Развитие элементарных математических представлений у детей 4 5 лет: Картотека дидактических игр по формированию элементарных математических представлений детей 4-5 лет | Картотека (средняя группа):
Картотека дидактических игр по формированию элементарных математических представлений детей 4-5 лет | Картотека (средняя группа):
Муниципальное автономное дошкольное образовательное учреждение
детский сад № 16 г.Туймазы муниципального района
Туймазинский район Республики Башкортостан
Картотека
дидактических игр по формированию элементарных математических представлений детей 4-5 лет
Выполнил:
Воспитатель Саитгареева Э.Р.
Имеющаяся категория: первая
Стаж работы: 17 лет
г.Туймазы – 2019г.
Количество и счет
1. Дидактическая игра: «Правильный счет»
Цель: помочь усвоению порядка следования чисел натурального ряда; закреплять навыки прямого и обратного счета.
Оборудование: мяч.
Содержание: дети встают в круг. Перед началом договариваются, в каком порядке (прямом или обратном) будут считать. Затем бросают мяч и нанизывают число. Тот, кто поймал мяч, продолжает счет, перебрасывая мяч следующему игроку
2.![]() Дидактическая игра: «Много-мало»
Дидактическая игра: «Много-мало»
Цель: помочь усвоить понятия «много», «мало», «один», «несколько», «больше», «меньше», «поровну».
Содержание: попросить ребенка назвать одиночные предметы или предметы, которых много (мало). Например: стульев много, стол один, книг много, животных мало. Положить перед ребенком карточки разного цвета. Пусть зеленых карточек будет-7, а красных -5. Спросить каких карточек больше, каких меньше. Добавить еще 2 красные карточки. Что теперь можно сказать?
3. Дидактическая игра: «Отгадай число»
Цель: способствовать подготовке детей к элементарным математическим действиям сложения и вычитания; помочь закрепить навыки определения предыдущего и последующего числа в пределах первого десятка.
Содержание: спросить, например, какое число больше трех, но меньше пяти; какое число меньше трех, но больше единицы и т. д. Задумать, например, число в пределах десяти и попросить ребенка отгадать его. Ребенок называет разные числа, а воспитатель говорит больше или меньше задуманного названное число. Затем можно поменяться с ребенком ролями.
Затем можно поменяться с ребенком ролями.
4. Дидактическая игра: «Счетная мозаика»
Цель: познакомить с цифрами; учить устанавливать соответствие количества с цифрой.
Оборудование: счетные палочки.
Содержание: вместе с ребенком составлять цифры с помощью счетных палочек. Предложить ребенку рядом с поставленной цифрой поместить соответствующее ей количество счетных палочек.
5. Дидактическая игра: «Читаем и считаем»
Цель: помочь усвоить понятия «много», «мало», «один», «несколько», «больше», «меньше», «поровну», «столько», «сколько»; умение сравнивать предметы по величине; умение считать в пределах 5.
Оборудование: счетные палочки.
Содержание: читая ребенку книжку, попросить его отложить столько счетных палочек, сколько, например, было зверей в сказке. После того как сосчитали, сколько в сказке зверей, спросить, кого было больше, кого – меньше, а кого – одинаково. Сравнить игрушки по величине: кто больше –зайка или мишка? Кто меньше? Кто такого же роста?
6. Дидактическая игра «Возьми столько же»
Дидактическая игра «Возьми столько же»
Цель: упражнять в составлении двух равных групп предметов, активизировать словарь «столько же», «поровну».
Оборудование. У детей таблица с тремя полосками, деленная по вертикали на три равные части.
Содержание: В левой части карточки изображены разные предметы (от 1 до 5, наборы геометрических фигур и счетных палочек.
Педагог предлагает рассмотреть таблицы и рассказать, что на них нарисовано. Затем дети заполняют среднюю (по вертикали) часть таблицы, берут столько же геометрических фигур, сколько предметов изображено в каждой клетке. Педагог спрашивает ребенка, сколько фигур он положил, предлагает проверить правильность путем наложения. После заполнения средней части таблицы дети берут счетные палочки и выкладывают в правой части таблицы по количеству нарисованных предметов.
7. Дидактическая игра «Кому сколько?»
Цель: Усвоить понятие «сколько»
Содержание: Ведущий раздает карточки с нарисованными мальчиками и девочками и их одеждой, а на стол кладет карточку с двумя девочками и спрашивает: «Сколько им надо шапочек?» Дети отвечают: «Две». Тогда ребенок, у которого на руках картинка с двумя шапочками, кладет ее рядом с карточкой, где нарисованы две девочки, и т. д. В присчитывании и отсчитывании дети упражняются в играх с мелкими игрушками. Игра состоит в том, что ребенок, получив карточку с нарисованными кружочками и сосчитав их, отсчитывает себе столько игрушек, сколько кружочков на карте. Затем карты смешиваются и снова раздаются. Дети пересчитывают на своих картах кружочки и, если их больше, чем отобрано игрушек по первой карте, решают, сколько еще надо прибавить игрушек или отнять, если кружочков меньше. Игрушек на столе должно быть много. А кружочков на маленьких карточках пять (1, 2, 3, 4, 5). Это число кружочков в карточках может несколько раз повторяться.
Тогда ребенок, у которого на руках картинка с двумя шапочками, кладет ее рядом с карточкой, где нарисованы две девочки, и т. д. В присчитывании и отсчитывании дети упражняются в играх с мелкими игрушками. Игра состоит в том, что ребенок, получив карточку с нарисованными кружочками и сосчитав их, отсчитывает себе столько игрушек, сколько кружочков на карте. Затем карты смешиваются и снова раздаются. Дети пересчитывают на своих картах кружочки и, если их больше, чем отобрано игрушек по первой карте, решают, сколько еще надо прибавить игрушек или отнять, если кружочков меньше. Игрушек на столе должно быть много. А кружочков на маленьких карточках пять (1, 2, 3, 4, 5). Это число кружочков в карточках может несколько раз повторяться.
Геометрическая форма
1. Дидактическая игра: «Подбери по форме»
Цель: учить детей выделять форму предмета, отвлекаясь от других его признаков.
Оборудование. по одной крупной фигуре каждой из пяти геометрических форм, карточки с контурами геометрических фигур по две фигуры каждой формы двух величин разного цвета (большая фигура совпадает с контурным изображением на карточке) .
Содержание: детям раздаются фигуры и карточки. Воспитатель: «Мы сейчас будем играть в игру «Подбери по форме». Для этого нам надо вспомнить названия разных форм. Какой формы эта фигура? (далее этот вопрос повторяется с показом других фигур). Вы должны разложить фигуры по форме, не обращая внимания на на цвет». Детям, неправильно разложившим фигуры, педагог предлагает обвести пальцем контур фигуры, найти и исправить ошибку.
2. Дидактическая игра: «Лото»
Цель: освоение умений выделять различные формы.
Оборудование: карточки с изображением геометрических фигур.
Содержание. Детям раздают карточки, на которых в ряд изображены 3 геометрические фигуры разного цвета и формы. Карточки отличаются расположением геометрических фигур, сочетанием их по цвету. Детям по одной предъявляются соответствующие геометрические фигуры. Ребенок, на карточке которого имеется предъявленная фигура, берет ее и накладывает на свою карточку так, чтобы фигура совпала, с нарисованной. Дети говорят, в каком порядке расположены фигуры.
3. Дидактическая игра: «Найди свой домик»
Цель: закреплять умение различать и называть круг, треугольник, прямоугольник, квадрат.
Оборудование: 4 обруча, круги, квадраты, треугольники, прямоугольники по количеству детей, бубен.
Содержание: Воспитатель кладет на пол два обруча на большом расстоянии друг от друга. Внутри первого обруча он помещает вырезанный из картона квадрат, внутри второго – круг. Детей надо разделить на две группы: у одних в руках квадрат, а у других – круг. Затем воспитатель объясняет правила игры, которые заключаются в том, что ребята бегают по комнате, а когда он ударит в бубен, должны найти свои домики. Те, у кого круг, бегут к обручу, где лежит круг, а те, у кого квадрат, — к обручу с квадратом.
Когда дети разбегутся по местам, воспитатель проверяет, какие фигуры у детей, правильно ли они выбрали домик, уточняет, как называются фигуры и сколько их. При повторном проведении игры надо поменять местами фигуры, лежащие внутри обручей.
4. Дидактическая игра: «Отгадай»
Дидактическая игра: «Отгадай»
Цель: закреплять умение различать круг, квадрат и треугольник.
Оборудование: мяч; круги, квадраты, треугольники разных цветов.
Содержание: Дети становятся в круг, в центре которого находится воспитатель с мячом. Он говорит, что сейчас все будут придумывать, на что похож тот предмет, который будет показан. Вначале воспитатель показывает желтый круг и кладет его в центр. Затем предлагает подумать и сказать, на что этот круг похож. Отвечает тот ребенок, которому воспитатель покатит мяч. Ребенок, поймавший мяч, говорит, на что похож круг. Например, на блин, на солнце, на тарелку…Далее педагог показывает большой красный круг. Дети фантазируют: яблоко, помидор…В игре принимают участие все. Для того чтобы детям был более понятен смысл игры «Отгадай», покажите им иллюстрации. Так, красный круг – помидор, желтый круг – мяч.
Величины.
1. Дидактическая игра: «Сбор фруктов»
Цель: развивать глазомер при выборе по образцу предметов определённой величины.
Оборудование: яблоки образцы (вырезанные из картона) трёх величин большие, поменьше, маленькие; три корзины большая, поменьше, маленькая; дерево с подвешенными картонными яблоками такой же величины, что и образцы (по 8-10 яблок были одной величины). Диаметр каждого яблока меньше предыдущего на 0, 5 см.
Содержание: воспитатель показывает дерево с яблоками, корзины и говорит, что маленькие яблоки надо собрать в маленькую корзиночку, а большие в большую. Одновременно вызывает троих детей, каждому даёт по яблоку образцу и предлагает им сорвать по одному такому же яблоку с дерева. Если яблоки сорваны правильно, педагог просит положить их в соответствующие корзинки. Затем задание выполняет новая группа детей. Игру можно повторить несколько раз.
2. Дидактическая игра:»Раз, два, три — ищи!»
Цель: научить детей строить образ предмета заданной величины и использовать его в игровых действиях.
Оборудование: Одноцветные пирамидки (желтые и зеленые, с количеством колец не менее семи. 2-3 пирамидки каждого цвета.
2-3 пирамидки каждого цвета.
Содержание: Дети усаживаются на стульчики полукругом. В. раскладывает на 2-3 столах пирамидки, перемешивая колечки. Две пирамидки ставит на маленький столик перед детьми и разбирает одну из них. Затем вызывает детей и каждому ин них дает по колечку одного размера и просит найти пару к своему колечку. «Посмотрите внимательно на свои колечки и постарайтесь запомнить, какого они размера, чтобы не ошибиться. Какое у тебя колечко, большое или маленькое? Если ребенок затрудняется с ответом, В. предлагает подойти к собранной пирамидке и приложить свое колечко к колечку такой величины. Затем детям предлагает оставить свои колечки на стульчиках и отправиться на поиски других колечек такой же величины. Искать колечки нужно только после того, как все дети скажут такие слова» Раз, два, три-ищи!» Выбрав колечко, каждый ребенок возвращается на место и накладывает его на свой образец, который остался на стульчике. Если ребенок ошибся, ему разрешается исправить ошибку, заменив выбранное колечко на другое. Для разнообразия при повторении игры можно использовать как образец пирамидку другого цвета.
Для разнообразия при повторении игры можно использовать как образец пирамидку другого цвета.
3. Дидактическая игра: » У кого хвост длиннее?»
Цель: Освоение умения сравнивать предметы контрастных размеров по длине и ширине, использовать в речи понятия: «длинный», «длиннее», «широкий», «узкий.
Содержание. Шум за дверью. Появляются звери: слоненок, зайчик, медведь, обезьяна – друзья Вини-Пуха. Звери спорят, у кого длиннее хвост. Винни-Пух предлагает детям помочь зверям. Дети сравнивают длину ушей зайца и волка, хвостов лисы и медведя, длину шеи жирафа и обезьяны. Каждый раз вместе с В. они определяют равенство и неравенство по длине и ширине, пользуясь соответствующей терминологией: длинный, длиннее, широкий, узкий и т. д.
4. Дидактическая игра: «Кто скорее свернет ленту»
Цель: продолжать формировать отношение к величине как к значимому признаку, обратить внимание на длину, знакомить со словами «длинный», «короткий».
Содержание. Воспитатель предлагает детям научиться свертывать ленту и показывает как это надо сделать, дает каждому попробовать. Затем предлагает поиграть в игру «Кто скорее свернет ленту». Вызывает двоих детей, дает одному длинную, другому короткую ленту и просит всех посмотреть, кто первый свернет свою ленту. Естественно, побеждает тот, у кого лента короче. После этого педагог раскладывает ленты на столе так, чтобы разница их была хорошо видна детям, но ничего не говорит. Затем дети меняются лентами. Теперь выигрывает другой ребенок. Дети садятся на место, педагог вызывает детей и предлагает одному из них выбрать ленту. Спрашивает, почему он хочет эту ленту. После ответов детей называет ленты «короткая», «длинная» и обобщает действия детей: «Короткая лента свертывается быстро, а длинная медленно».
Затем предлагает поиграть в игру «Кто скорее свернет ленту». Вызывает двоих детей, дает одному длинную, другому короткую ленту и просит всех посмотреть, кто первый свернет свою ленту. Естественно, побеждает тот, у кого лента короче. После этого педагог раскладывает ленты на столе так, чтобы разница их была хорошо видна детям, но ничего не говорит. Затем дети меняются лентами. Теперь выигрывает другой ребенок. Дети садятся на место, педагог вызывает детей и предлагает одному из них выбрать ленту. Спрашивает, почему он хочет эту ленту. После ответов детей называет ленты «короткая», «длинная» и обобщает действия детей: «Короткая лента свертывается быстро, а длинная медленно».
5. Дидактическая игра «Сравни дорожки»
Оборудование: Дорожки (полоски) разной ширины.
Цель: Учить сравнивать предметы по ширине, раскладывать их в убывающей и возрастающей последовательности, обозначать результаты сравнения соответствующими словами: широкий, уже, самый узкий, узкий, шире, самый широкий.
Содержание: Педагог предлагает сравнить дорожки разными способами (приложением, наложением, разложить в порядке увеличения ширины, уменьшения.
Ориентирована в пространстве
1. Дидактическая игра: «Кто где»
Цель: учить различать положение предметов в пространстве (впереди, сзади, между, посредине, справа, слева, внизу, вверху).
Оборудование: игрушки.
Содержание: расставить игрушки в разных местах комнаты. Спросить ребенка, какая игрушка стоит впереди, позади, рядом, далеко и т. д. Спросить, что находится сверху, что снизу, справа, слева и т. д.
2. Дидактическая игра: «Бегите к цифре»
Цель: упражнять в запоминании и различении цифр, умении ориентироваться в пространстве; развивать слуховое и зрительное внимание.
Оборудование: карточки с изображением цифр, развешанные в разных местах комнаты.
Содержание: Игра малой подвижности. Педагог (водящий) называет одну из цифр, дети находят в помещении карточку с ее изображением и бегут к ней. Если какой-то ребенок ошибается, он выбывает из игры на некоторое время. Игра проводится до тех пор, пока не выявится победитель.
Если какой-то ребенок ошибается, он выбывает из игры на некоторое время. Игра проводится до тех пор, пока не выявится победитель.
Можно усложнить задание, предложив детям, встав около цифры, прохлопать в ладоши (или протопать, или присесть) число, которое она обозначает.
3. Дидактическая игра: «Лифт»
Цель: закреплять прямой и обратный счет до 5, закрепление основных цветов радуги, закреплять понятия «вверх», «вниз», запоминать порядковые числительные (первый, второй)
Содержание: Ребенку предлагается помочь жителям поднять или опустить их на лифте, на нужный этаж, считать этажи, узнать, сколько живет жильцов на этаже.
4. Дидактическая игра: «Три шага»
Цель: ориентировка в пространстве, умение слушать и выполнять инструкции.
Содержание: Игроки разбиваются на две равные команды, встают друг за другом. Задача каждой команды – полным составом, ровно, строго следуя правилам, как можно быстрее достичь финиша: произносят хором правила: три шага влево, три шага вправо, шаг вперед, один назад и четыре прямо.
5. Дидактическая игра «Что где находится?»
Цель: Упражнять в определении пространственного расположения предметов по отношению от себя «впереди», «сзади», «перед», «слева», «справа», «вверху», «внизу».
Оборудование: Игрушки
Содержание: Ребенок останавливается в определенном месте комнаты и пересчитывает предметы находящиеся впереди, сзади, слева, справа.
6. Дидактическая игра «Футбольное поле»
Цель: учить различать положение предметов в пространстве (посредине, справа, слева, внизу, вверху).
Оборудование: листы бумаги и маленькие круги по количеству детей.
Содержание: Детям предлагается поиграть в футбол на бумаге. По заданию педагога круг («мяч») выкладывается в определенное место листа («поля»): верхний левый угол, нижний правый угол, середина «поля» и т. д.
Ориентирована во времени
1. Дидактическая игра: «Когда это бывает»
Цель: закреплять знания детей о временах года, их характерных признаках; развивать связную речь, внимание и находчивость, выдержку.
Оборудование: картинки по временам года.
Содержание: Дети сидят вокруг стола. У воспитателя в руках несколько картинок с изображением разных времён года, для каждого времени года по 2-3 картинки. Воспитатель разъясняет правила игры, воспитатель раздаёт всем по картинке. Затем вращает стрелку по кругу. Тот, на кого она указала, внимательно рассматривает свою картинку и затем рассказывает о её содержимом. Затем опять крутят стрелку и тот на кого она указала угадывает время года. Вариантом этой игры может быть чтение воспитателем отрывков из художественных произведений о сезонных природных явлениях и поиск картинок с соответствующим содержанием.
2. Дидактическая игра: «Назови пропущенное слово»
Цель: учить называть временные отрезки: утро, вечер, день, ночь.
Оборудование: мяч.
Содержание: Дети образуют полукруг. Воспитатель катит кому-нибудь из детей мяч. Начинает предложение, пропуская названия частей суток: — Мы завтракаем утром, а обедаем. Дети называют пропущенное слово. — Утром ты приходишь в детский сад, а уходишь домой ….-Днем ты обедаешь, а ужинаешь…
— Утром ты приходишь в детский сад, а уходишь домой ….-Днем ты обедаешь, а ужинаешь…
3. Дидактическая игра: «Кто раньше? Кто позже?»
Цель: закреплять знания детей о временных представлениях: сначала, потом, до, после, раньше, позже.
Содержание: Инсценировка сказок с использованием иллюстраций «Репка», «Теремок», «Колобок» и др.
4. Дидактическая игра: «Светофор»
Цель: закреплять представления детей о временах года.
Содержание: Педагог говорит, например, «Кончилось лето, наступила весна». Дети поднимают красный круг – сигнал остановки, ошибки исправляются.
5. Дидактическая игра: «Когда это бывает?»
Цель: закреплять знания детей о частях суток, их последовательности, закреплять понятия — вчера, сегодня, завтра.
Содержание: Дети в кругу. Ведущий начинает фразу и бросает мяч одному из играющих: «Солнышко светит днем, а луна ….». Тот, кто заканчивает фразу, придумывает новую «Утром мы пришли в детский сад, а вернулись …», «Если вчера была пятница, то сегодня …», «Зиму сменяет весна, а весну …».
6. Дидактическая игра «Вчера, сегодня, завтра»
Цель: Закреплять понятие о таких категориях, как «вчера», «сегодня», «завтра»
Материал: Мяч
Содержание: Ведущий бросает мяч по очереди всем играющим и говорит: «Мы лепили. когда». Поймавший заканчивает фразу, как бы отвечает на вопрос «когда?»
Мы пойдем гулять в парк. (сегодня)
Мы навещали бабушку. (вчера)
Мы будем читать книгу. (завтра)
Дидактическая игра «Что изменилось?»
Цель: развить внимание и память детей.
Содержание: Дети образуют круг. Внутри круга стоят несколько детей. По знаку воспитателя один уходит, затем, войдя, он должен определить, какие изменения произошли внутри круга. В этом варианте отгадывающий ребенок должен подсчитать, сколько детей стояло в кругу вначале, сколько осталось, и, сопоставив эти два числа, определить, сколько детей ушло из круга. Затем при повторении игры отгадывающий должен назвать имя ушедшего ребенка. А для этого требуется удержать в памяти имена всех стоящих в кругу детей и, посмотрев на оставшихся, установить, кого нет. Дальнейшее усложнение может быть таким: число детей в кругу остается то же (в пределах пяти, но изменяется их состав. Отгадывающий должен сказать, кто из детей ушел и кто встал на его место. Этот вариант требует от детей больше внимания и наблюдательности.
Дальнейшее усложнение может быть таким: число детей в кругу остается то же (в пределах пяти, но изменяется их состав. Отгадывающий должен сказать, кто из детей ушел и кто встал на его место. Этот вариант требует от детей больше внимания и наблюдательности.
Как развивать математические способности у детей: самые эффективные методы
Зачем учить математику
«Математику уже затем учить надо, что она ум в порядок приводит». М.В. Ломоносов
Математика – уникальный предмет. Она незаменима для развития у детей:
- логического мышления;
- памяти;
- речи;
- воображения.
Участвует в формировании настойчивости, терпения, творческих способностей личности. Учит анализу и синтезу, планированию своих действий, максимально точному изложению мыслей, умению обосновывать имеющуюся точку зрения. Помогает знакомить детей дошкольного возраста с окружающим миром.
Знания математического содержания нужны ребёнку для успешности социальной адаптации, а также, для ориентировании во всё более развивающихся информационных и технологических процессах в обществе.
С какого возраста и как обучать
Пяти-, шестилетки весьма активны в вопросах познания и освоения окружающей их действительности. Дети дошкольного возраста очень любят задавать вопросы, особенно любимым становится вопрос «почему?». Они стараются разобраться в устройстве какой-либо вещи, начинают устанавливать причину и следствие каких-либо событий, происходящих вокруг. Эти вопросы и навыки весьма полезны не только для общего развития, но и для обучения. Поэтому с 5-6 лет уже можно активно обучать их математике. Бывает, что ребёнок и более младшего возраста (3-4 лет) также интересуется предметом. В этом случае, не нужно дожидаться достижения им 5-6 лет, чтобы приступить к занятиям.
Знакомство с цифрами можно начинать с 3-х лет
Следуйте за интересами своего дошкольника, прислушивайтесь к нему, старайтесь сохранить его естественный природный интерес к предмету. Ваши старания будут вознаграждены. В то же время ни в коем случае не следует «навязывать» детям необходимость изучать предмет, т.к. можно добиться обратного эффекта – нежелания учиться, отсутствия заинтересованности.
Ваши старания будут вознаграждены. В то же время ни в коем случае не следует «навязывать» детям необходимость изучать предмет, т.к. можно добиться обратного эффекта – нежелания учиться, отсутствия заинтересованности.
Основной вид деятельности дошкольников – это игра, поэтому при обучении и следует пользоваться всем многообразием её возможностей. Не следует стремиться проводить с ребёнком полноценные занятия, как в детском саду или центре. У вас в приоритете должны быть совсем другие формы: прогулки, экскурсии, игры с природными материалами (водой, песком), конструкторы, совместные занятия домашними делами, чтение и знакомство с элементами фольклора (считалками, скороговорками), настольные игры, ситуационные игры (магазин, поезд) – в общем, всё, что подскажет ваша фантазия, воображение, жизненный опыт.
Математическая игра “Рыбка” – интересное обучение
Совет родителям: ко времени поступления в первый класс ваш малыш должен освоить применение знаний математики в важных для него практических занятиях: играх, экспериментах, быту.
Какие способности относятся к математическим у детей до 7-ми лет
Не стоит думать, что математические способности подразумевают под собой только умение быстро и точно считать. Это заблуждение. Математические способности включают в себя целый комплекс умений, направленных и на творческий подход, и логику, и счет.
Быстрота подсчета, способность запоминать большой массив цифр и данных не являются подлинными математическими способностями, так как даже медленный и обстоятельный ребенок, который вдумчиво занимается может успешно постигать математику.
К математическим способностям относится:
- Способность обобщения математического материала.
- Умение видеть общее у разных предметов.
- Возможность найти главное в большом количестве различной информации и исключить не нужное.
- Пользоваться числами и знаками.
- Логическое мышление.
- Способность ребенка мыслить абстрактными структурами. Умение отвлечься от решаемой задачи и увидеть полученную картину в целом.

- Мыслить как прямо, так и в обратной последовательности.
- Умение самостоятельно мыслить, не используя шаблонов.
- Развитая математическая память. Способность использовать полученные знания в различных ситуациях.
- Пространственное мышление – уверенное использование понятий «верх», «низ», «право» и «лево».
Элементарные математические представления дошкольников
Малышей необходимо обучать счету, знакомить с количественными соотношениями, расширять познания геометрических фигур. К концу дошкольного возраста ребенок должен иметь базовые математические представления:
- Знать все цифры от 0 до 9 и узнавать их в любой форме написания.
- Считать от 1 до 10, как в прямом, так и обратном порядке (начиная с любой цифры).

- Иметь представление о простых порядковых числительных и уметь ими оперировать.
- Выполнять операции сложения и вычитания в пределах 10.
- Уметь уравнивать количество предметов в двух наборах (В одной корзинке 5 яблок, в другой – 7 груш. Что нужно сделать, чтобы фруктов в корзинках было поровну?).
- Знать основные геометрические фигуры и называть отличающие их признаки.
- Оперировать количественными соотношениями «больше-меньше», «дальше-ближе».
- Оперировать простыми качественными соотношениями: самый большой, самый маленький, самый низкий и пр.
- Понимать сложные отношения: «больше, чем самый маленький, но меньше других», «впереди и выше других» и пр.
- Уметь выявлять лишний объект, не подходящий к группе остальных.
- Выстраивать простые ряды по возрастанию и убыванию (На кубиках изображены точки в количестве 3, 5, 7, 8. Расставить кубики так, чтобы количество точек на каждом последующем уменьшалось).
- Находить соответствующее место объекта с числовым признаком (На примере предыдущего задания: расставлены кубики с точками 3, 5 и 8.
 Куда поставить кубик с 7 точками?).
Куда поставить кубик с 7 точками?).
Этот математический «багаж» предстоит накопить ребенку до поступления в школу. Перечисленные представления относятся к элементарным. Без них изучать математику невозможно.
Среди базовых умений есть совершенно простые, которые доступны уже в 3-4 года, но есть и такие (9-12 пункты), которые используют простейший анализ, сравнение, обобщение. Им предстоит сформироваться в процессе игровых занятий в старшем дошкольном возрасте.
Перечень элементарных представлений можно использовать для выявления математических способностей дошкольников. Предложив ребенку выполнить задание, соответствующее каждому пункту, определяют, какие умения уже сформированы, а над какими нужно поработать.
Необходимые знания и навыки
Перед поступлением в 1 класс дети должны освоить определенные умения — владеть карандашом и ручкой, уметь штриховать, рисовать и раскрашивать, познакомиться с буквами. На занятиях же математикой им нужно будет научиться еще большему:
- разобраться с такими понятиями как число и множество, форма предмета, величина;
- освоить навык ориентирования в пространстве;
- получить навыки счета, измерения и сравнения;
- научиться оперировать некоторыми математическими терминами (больше-меньше, равно, узкий-широкий, длинный-короткий и т.
 п.).
п.).
В процессе занятий у детей формируются навыки анализа и синтеза, обобщения и сравнения, расширяется активный речевой словарь. Само постепенное формирование математических представлений не только способствует боле успешному обучению детей в школе, но и развивает мышление. Поэтому дидактическим математическим играм уделяется значительное внимание.
Особенно это важно для детей, имеющих нарушения в развитии речи. Недостаточно развитый словарь, нередко сопутствующее отставание формирования высшей нервной деятельности приводят к тому, что детям труднее даются математические упражнения. Важно уделять в том случае играм большее внимание, соблюдая правило «от простого к сложному». Индивидуальный подход играет значительную роль, позволяя ребенку осваивать необходимые навыки в нужном ему темпе.
Каким образом формируются математические способности
Все способности, в том числе и математические, не являются предопределенным навыком. Они формируются и развиваются через обучение и закрепляются практикой.
Любая способность проходит несколько этапов в своем развитии:
- Познание. Ребенок знакомится с предметом и узнает необходимый материал;
- Применение. Применяет новые знания в самостоятельной игре;
- Закрепление. Возвращается к занятиям и повторяет ранее изученное;
- Применение. Использование закрепленного материала при самостоятельной игре;
- Расширение. Происходит расширение знания о предмете или способности;
- Применение. Ребенок дополняет самостоятельную игру новым знанием;
- Адаптация. Знание переносится из игровой ситуации в жизнь.
Любое новое знание должно пройти несколько раз через этап применения. Давайте ребенку возможность использовать полученные данные в самостоятельной игре. Детям нужно некоторое время, чтобы осмыслить и закрепить каждое незначительное изменение в знаниях.
В случае, если ребенок не сможет через самостоятельную игру усвоить полученный навык или знание, высока вероятность того, что оно не будет закреплено. Поэтому после каждого занятия отпускайте малыша поиграть или отвлекитесь, поиграйте с ним. Во время игры покажите, как использовать новые знания.
Как развить математические способности у ребенка
Начинать математическое развитие нужно в виде игры и использовать вещи, которые заинтересуют малыша. Например, игрушки и бытовые предметы, с которыми он сталкивается каждый день.
С того момента, когда ребенок проявит интерес к тому или иному предмету родитель начинает показывать ребенку, что предмет можно не только рассматривать и трогать, но и совершать с ним разные действия. Акцентируя внимание на некоторых признаках предмета (цвет, форма), в ненавязчивой манере можно показать разницу в количестве предметов, ввести первые понятия о множественном и пространственном положении.
После того, как ребенок научится разделять предметы по группам, можно показывать, что их можно считать и сортировать. Обратить внимание на геометрические особенности.
Обратить внимание на геометрические особенности.
Развитие математических способностей должно идти одновременно с основами операций с числами.
Любое новое знание должно быть преподнесено при явном интересе ребенка к обучению. При отсутствии заинтересованности в предмете и его изучении, обучение ребенка проводить не стоит. Важно соблюдать баланс в обучении ребенка, чтобы развивать любовь к математике. Практически все проблемы, связанные с изучением основ этой дисциплины, имеют свое начало в первоначальном отсутствии желания познать.
Математическое развитие детей раннего возраста
Когда происходит организация процесса педагогической работы с детьми раннего возраста, не стоит забывать, что сформировавшееся мнение у ребенка о математических значениях, геометрических фигурах, пространстве является одним из самых главных моментов познания мира, который его окружает. То, что вложится на данном этапе, будет играть значительную роль в будущих логических, умственных и математических способностях у ребенка. Исходя из этого, педагоги советуют при организации такого процесса в возрасте от двух до трех лет заниматься с ребенком не меньше двух раз в неделю. Очень важно помнить, что необходимо в эти занятия включать сенсорное развитие ребенка, оно имеет очень большой вес в обучении. После определенного изученного материала, не стоит забывать закреплять это в повседневных действиях:
Исходя из этого, педагоги советуют при организации такого процесса в возрасте от двух до трех лет заниматься с ребенком не меньше двух раз в неделю. Очень важно помнить, что необходимо в эти занятия включать сенсорное развитие ребенка, оно имеет очень большой вес в обучении. После определенного изученного материала, не стоит забывать закреплять это в повседневных действиях:
• Работа с конструктором.
• Лепка.
• Рисование.
• Игры для математического развития для детей.
• При прогулках.
Прежде, чем начать занятия с ребенком, необходимо тщательно подготовиться. Нужно подобрать средства занятия, которые смогут в течении 15-20 минут сосредоточить внимание малыша. Так же необходимо во избежание усталости ребенка менять действия в процессе. Главное в педагогических занятиях — уметь дозировать материал обучения, преподать его доступно и интересно для малыша раннего возраста. Не забывайте, что все обучение чаще всего должно происходить в игровой форме.
Игры для математического развития для детей:
1. Что двигается? Такая игра ознакомит малыша с предметами, их формами. Игра проходит в интересном и веселом соревновании. Из фигур строятся игрушечные ворота, кто быстрее докатит свою фигуру до них, тот и победил. Фигуры в свою очередь должны быть в виде шаров и кубиков. Очень важно помнить, что в этой игре нельзя поддаваться ребенку. Изначально малыш не будет обращать внимание на форму фигуры, и ему будет не важно, какой играть. Но в дальнейшем он начнет понимать, что шарик катить удобней и он постоянно побеждает — будет стремиться выбрать именно эту фигуру. Не упустите этот момент, и задайте вопрос, почему ребенок желает играть именно шаром, и постарайтесь вместе логически поразмышлять. Например, что углы у кубика острые и мешают так быстро двигаться как шарик.
Что двигается? Такая игра ознакомит малыша с предметами, их формами. Игра проходит в интересном и веселом соревновании. Из фигур строятся игрушечные ворота, кто быстрее докатит свою фигуру до них, тот и победил. Фигуры в свою очередь должны быть в виде шаров и кубиков. Очень важно помнить, что в этой игре нельзя поддаваться ребенку. Изначально малыш не будет обращать внимание на форму фигуры, и ему будет не важно, какой играть. Но в дальнейшем он начнет понимать, что шарик катить удобней и он постоянно побеждает — будет стремиться выбрать именно эту фигуру. Не упустите этот момент, и задайте вопрос, почему ребенок желает играть именно шаром, и постарайтесь вместе логически поразмышлять. Например, что углы у кубика острые и мешают так быстро двигаться как шарик.
2. Одеваем кукол. Дети раннего возраста довольно быстро начинают ориентироваться в размерах предметов, их однотипности. Для этой игры необходимо дать две куклы разных размеров и два вида одежды (побольше и поменьше). Не говорите ребенку, какой из комплектов принадлежит большой кукле, а какой — маленькой, просто предложите ему одеть своих кукол. Ребенок сам должен это определить, в этом и заключается суть игры. Не расстраивайтесь, если с первого раза ребенок оденет их наоборот, начните с ним логический разговор, о том, что платье мало или велико.
Ребенок сам должен это определить, в этом и заключается суть игры. Не расстраивайтесь, если с первого раза ребенок оденет их наоборот, начните с ним логический разговор, о том, что платье мало или велико.
3. Собираем урожай. Например, сбор яблок, для этого подойдут любые шарообразные предметы разной формы. Разлаживаем их по разным коробкам в зависимости от размеров (большие — к большим, средние — к средним, маленькие — к маленьким). Урожай можно выбрать любой, лучше всего, опираясь на предпочтения ребенка, так ему будет интересней.
4. Найди одинаковый. Разложите разные фигуры и предложите ребенку из всех выбрать одинаковый по цвету, размеру и форме с тем, который вы будете держать. В такой игре Вам можно делать ошибки и указывать на них, чтобы в дальнейшем ребенок сам замечал и указывал вам на эти ошибки.
5. Что загадали. В данной игре малыш учится ориентироваться в пространстве. Родителям понадобятся различные игрушки больших размеров (подойдут и куклы, и мягкие зайчики, мишки). Малыша посадите в центр, а выбранные игрушки — вокруг него. Родители загадывают любую из игрушек, а ребенок должен ее отгадать, основываясь на подсказки от папы и мамы. Например, где сидит игрушка – сбоку, сзади или спереди, какого цвета и т.д. Если малыш с легкостью угадывает, попробуйте усложнить подсказки. Важно заставить ребенка думать.
Малыша посадите в центр, а выбранные игрушки — вокруг него. Родители загадывают любую из игрушек, а ребенок должен ее отгадать, основываясь на подсказки от папы и мамы. Например, где сидит игрушка – сбоку, сзади или спереди, какого цвета и т.д. Если малыш с легкостью угадывает, попробуйте усложнить подсказки. Важно заставить ребенка думать.
6. Покажи по-разному. Для данной игры необходимо минимум два ребенка. Одно и тоже слово, фигуру дети должны показать в разной интерпретации. Так ребенок знакомится с антонимами и в то же время учится мыслить.
Математическое развитие детей 3-4 лет
Многие взрослые считают, что не стоит нагружать детей 3-4 лет такой сложной наукой, как математика. По их мнению, для этого придуманы школы — это очень ошибочное решение. В таком раннем возрасте не стоит задача научить ребенка считать уравнения и примеры, стоит задача научить малыша логически мыслить, заставить ребенка думать перед каждым своим действием.
В этом возрасте уже можно учить ребенка количеству, величине, геометрическим фигурам, ориентированию в пространстве, ориентированию во времени. Все обучение проходит в игровой форме, с обязательным повторением для закрепления материала.
Все обучение проходит в игровой форме, с обязательным повторением для закрепления материала.
Математическое развитие детей в семье
Логико-математическое развитие ребенка в семье происходит под управлением взрослого человека и постепенно. В процесс развития входят постоянные занятия, которые направлены на ориентирование в пространстве, изучение количественного значения, ориентирование во времени. Детям дошкольного возраста обязательны основы математики.
Из чего же состоит логико-математическое развитие детей дошкольного возраста:
1. Изучение количества (сложение, вычитание, сравнение, умножение, деление и т.д.). Но это только арифметика, многие думают, что на этом математическое развитие должно быть окончено. Это большая ошибка. Есть еще масса дисциплин в этом процессе.
2. Геометрия. Название говорит само за себя. Это процесс изучения фигур, их формы, цвет, размеры и т.д.
3. Математику понять не сложно, достаточно разобраться в ее признаках, особенностях. Очень важно научиться классифицировать предметы по их признакам и особенностям, уметь сравнивать и видеть отличая. Существуют средства математического развития детей – их нужно иметь дома.
Очень важно научиться классифицировать предметы по их признакам и особенностям, уметь сравнивать и видеть отличая. Существуют средства математического развития детей – их нужно иметь дома.
4. Вторая самая важная дисциплина на начальном этапе развития – это, конечно же, логика. Если у ребенка не будет логического мышления, то и с математическими задачами ему справиться будет крайне сложно. Вначале это простая логика окружающего мира (все произошло так, потому что… или не произошло, если мы хотим чтобы что-то произошло, мы должны…, или наоборот и т.д.) Необходимо объяснять ребенку, что у всего происшедшего есть своя причина. Не забывайте обыгрывать ситуации.
Математическое развитие выполняется:
1. Ежедневно само по себе. В этом случае родители используют ситуации, которые произошли сами по себе в логико-математических целях. Например, мама на кухне готовит ужин и просит ребенка подать две луковицы — одну маленькую, вторую большую. Дети очень любят такие совместные работы. Аналогично можно использовать такую игру и при уборке, глажке и т. д.
д.
2. При обучении взрослыми. Важно не забывать, что маленькие дети воспринимают лучше всего эмоциональную информацию. При специальных занятиях используйте побольше стишков, игр, загадок, считалок, песенок. Игры – это основа обучения детей дошкольного возраста.
Методика математического развития детей дошкольного возраста довольно сложная и требует максимум времени и усилий. Все занятия и игры на первоначальном этапе не должны превышать 20-30 минут. Иначе ребенку станет не интересно, и второй раз его будет сложно заинтересовать. Не страшно, если игра будет длиться 10-15 минут, главное — не отбить у ребенка желание играть в дальнейшем.
Как заинтересовать детей математикой в начале занятия
Для активизации внимания своих воспитанников педагог может использовать в работе стихотворения, загадки, дидактические игры, костюмированные представления, демонстрацию иллюстраций, просмотр мультимедийных презентаций, видео или мультипликационных фильмов. Сюрпризный момент обычно выстраивается вокруг популярного и любимого детьми сказочного или литературного сюжета. Его герои создадут интересную ситуацию, оригинальную интригу, которая вовлечёт детей в игру или пригласит в фантастическое путешествие:
Его герои создадут интересную ситуацию, оригинальную интригу, которая вовлечёт детей в игру или пригласит в фантастическое путешествие:
Что делать, если ребенку неинтересно
Если ребенок при каждой попытке обучить его основам математики уходит и скучает, то нужно:
- Поменять форму преподнесения материала. Вероятнее всего ваши объяснения слишком сложные для понимания ребенком и не содержат игровых элементов. Дети дошкольного возраста не могут воспринимать информацию в классическом виде урока, им нужно показывать и рассказывать новый материал в ходе игры или развлечения. Сухой текст не воспринимается ребенком. Примените в обучении дидактические игры или попробуйте задействовать в обучении непосредственно ребенка;
- Проявите интерес к предмету без участия ребенка. Дети младшего возраста интересуются всем, что интересно их родителям. Они любят подражать и копировать взрослых. Если ребенок не проявляет интерес к какому-либо занятию, то попробуйте на глазах у ребенка начать играть с выбранными предметами.
 Вслух рассказывайте о том, что вы делаете. Показывайте собственную заинтересованность процессом игры. Ребенок увидит ваш интерес и присоединится;
Вслух рассказывайте о том, что вы делаете. Показывайте собственную заинтересованность процессом игры. Ребенок увидит ваш интерес и присоединится; - В случае, если ребенок все равно быстро теряет интерес к предмету, нужно проверить, не является ли то знание и умение, которое вы хотите ему привить, слишком сложным или легким;
- Помните о длительности занятий для разного возраста. Если ребенок до 4-х лет потерял интерес к предмету через 5 минут, то это нормально. Так как в этом возрасте ему сложно долго концентрироваться на одном предмете.
- Попробуйте вводить в занятие по одному элементу за раз. Для детей 5-7 лет длительность занятий не должна превышать 30 минут.
- Не стоит расстраиваться, если ребенок не захочет заниматься в конкретный день. Нужно попробовать привлечь его к обучению спустя некоторое время.
Главное, помнить:
- Материал должен быть адаптирован к возрасту ребенка;
- Родитель должен проявлять интерес к материалу и результатам ребенка;
- Ребенок должен быть готов к занятию.

Как развивать математическое мышление
Порядок научения ребенка математическому мышлению представляет собой связанные между собою занятия, которые преподносятся в порядке усложнения материала.
1. Начинать обучение нужно с понятий о пространственном расположении предметов
Ребенок должен понять, где находится право – лево. Что такое «выше», «ниже», «перед» и «за». Наличие этого навыка позволяет воспринимать все последующие занятия проще. Ориентирование в пространстве — основополагающее знание не только для развития математических способностей, но и для обучения ребенка чтению и письму.
Можно предложить ребенку следующую игру. Возьмите несколько его любимых игрушек и положите перед ним на разном расстоянии. Попросите его показать, какая игрушка находится ближе, какая дальше, какая левее и т.д. При появлении затруднений при выборе, подскажите правильный ответ. Используйте в этой игре различные варианты слов, которые определяют расположение предметов относительно малыша.
Употребляйте такой подход к изучению и повторению не только в процессе занятий, но и в обыденной жизни. Например, предложите ребенку определить пространственное расположение предметов на детской площадке. Чаще в обычной жизни обращайтесь с просьбой подать что-либо, ориентируя малыша в пространстве.
Параллельно с пространственным мышлением обучают обобщению и классификации предметов по их внешним признакам и функциональной принадлежности.
2. Изучите понятие множества предметов
Ребенок должен различать понятия много — мало, один — много, больше — меньше и поровну. Предложите игрушки разного вида в разном количестве. Предложите сосчитать их и сказать много их или мало, каких игрушек меньше и наоборот, также показывайте равенство игрушек.
Хорошая игра на закрепление понятия множества — «Что в коробочке». Ребенку предлагается две коробки или ящичка, в которых находится разное количество предметов. Путем перемещения предметов между коробками ребенку предлагается сделать количество предметов больше или меньше, уровнять. В возрасте до 3-х лет количество предметов не должно быть большим, чтобы ребенок мог наглядно оценить разницу в предметах без подсчета.
В возрасте до 3-х лет количество предметов не должно быть большим, чтобы ребенок мог наглядно оценить разницу в предметах без подсчета.
3. Важно в раннем детстве обучить ребенка простым геометрическим фигурам
Научите ребенка видеть их в окружающем мире. Хорошо для развития знания геометрических фигур использовать аппликации из математических форм. Покажите ребенку рисунок предмета с четкими контурами (дом, машина). Предложите сделать из заготовленных треугольников, квадратов и кругов образ предмета.
Покажите и объясните, что такое угол у фигур, предложите ребенку догадаться, почему «треугольник» носит такое имя. Предложите ребенку для ознакомления фигуры с большим количеством углов.
Закрепление геометрических знаний проведите через рисование изученного материала, складывания разных фигур из других предметов (палочек, камушков и т.д.). Можно использовать пластилин и другие материалы, позволяющие создавать различные формы.
Попросите нарисовать ряд фигур разного типа, посчитайте их вместе с ребенком. Спросите, каких фигур много, а каких мало.
Спросите, каких фигур много, а каких мало.
На прогулке с ребенком обратите внимание на форму домов, лавочек, машин и т.д. Покажите, как сочетание различных фигур между собой может создавать новые и знакомые предметы.
4. Умение ориентироваться в пространстве и классифицировать предметы позволяет научить измерению размера предмета
Раннее обучение измерения длины линейкой и при помощи сантиметров не рекомендуется, так как это будет сложный для восприятия материал. Попробуйте измерять предметы с ребенком при помощи палочек, ленточек и других подручных материалов. В этом обучении вложено не само измерение, а принцип его проведения.
Большинство педагогов советуют обучать ребенка измерению при помощи счетных палочек. Они обосновывают это удобством для ребенка и приучению его пользоваться специальным материалом. Эти палочки пригодятся при изучении единиц счета. Также их можно использовать как наглядный материал при работе с книгами (отложить палочку по количеству героев), изучении геометрических фигур (ребенок может выложить палочками нужную фигуру) и т. д.
д.
5. Количественные измерений
После изучения базовых математических понятий можно переходить к количественным измерениям и изучению чисел. Изучение чисел и их письменного обозначения происходит с раннего возраста по определенной системе.
6. Сложение и вычитание
Только после освоения количественных измерений и чисел стоит вводить сложение и вычитание. Сложение и вычитание вводится в возрасте 5-6 лет и представляет собой простейшие операции на одно действие с малыми числами.
7. Деление
Деление в дошкольном возрасте вводится только на уровне долей, когда ребенку предлагается разделить предмет на равные доли. Количество таких частей не должно превышать четырех.
8. Упражнения на развитие анализа и синтеза
1.По-порядку становись! Игра на упорядочение объектов по размеру. Подготовить 10 одноцветных полосок из картона одинаковой ширины и различной длины и разложить их хаотично перед дошкольником.
Инструкция: «Расставь «спортсменов» по росту от самого низкого до самого высокого». Если ребенок затрудняется с выбором полоски, предложите «спортсменам» мериться ростом.
Если ребенок затрудняется с выбором полоски, предложите «спортсменам» мериться ростом.
После выполнения задания предложите ребенку отвернуться и поменяйте местами некоторые полоски. Дошкольнику предстоит вернуть «хулиганов» на свои места.
2.Сложи квадрат. Подготовьте два набора треугольников. 1-ый — один большой треугольник и два маленьких; 2-ой – 4 одинаковых маленьких. Предложите ребенку сначала сложить квадрат из трех деталей, затем из четырех.
Рисунок 1.
Если дошкольник на составление второго квадрата затрачивает меньше времени, значит, пришло понимание. Способные дети справляются с каждым из этих заданий менее чем за 20 секунд.
9. Упражнения на абстрагирование и обобщение
1.Четвертый лишний. Понадобится набор карточек, на которых изображены четыре предмета. На каждой карточке три объекта должны быть связаны между собой существенным признаком.
Инструкция: «Найди, что на картинке лишнее. Что не подходит ко всем остальным и почему?».
Рисунок 2.
Такие упражнения стоит начинать с простых групп объектов и постепенно усложнять. Например, карточку с изображением стола, стула, чайника и дивана – можно применять в занятиях с 4-летними детьми, а наборы с геометрическими фигурами предлагать старшим дошкольникам.
2.Построй заборчик. Необходимо подготовить не менее 20 полосок равной длины и ширины или счетные палочки двух цветов. Для примера: синего цвета – С, и красного – К.
Инструкция: «Давай построим красивый заборчик, где чередуются цвета. Первой будет синяя палочка, за ней – красная, далее… (продолжаем выкладывать палочки в последовательности СКССККСК). А теперь ты продолжи строить забор, чтобы был такой же узор».
В случае затруднения обращать внимание ребенка на ритм чередования цветов. Упражнение можно выполнять несколько раз с различным ритмом узора.
10. Логико-математические игры
1.Мы едем-едем-едем. Необходимо подобрать 10-12 прямоугольных картинок с изображением хорошо знакомых ребенку предметов. Играет ребенок в паре с взрослым.
Играет ребенок в паре с взрослым.
Инструкция: «Сейчас мы составим поезд из вагончиков, которые будут прочно между собой связаны важным признаком. В моем вагончике будет чашка (кладет первую картинку), а чтобы твой вагончик присоединился, можно выбрать картинку с изображением ложки. Чашка и ложка связаны, потому что это посуда. Я дополню наш поезд картинкой с совочком, так как совочек и ложка имеют похожую форму и т.д.»
Поезд готов отправиться в путь, если все картинки нашли свое место. Можно смешать картинки и вновь начать игру, находя новые взаимосвязи.
2.Почини коврик. Задания на поиск подходящей «заплатки» для коврика вызывают живой интерес у дошкольников разного возраста. Для проведения игры необходимо изготовить несколько картинок, на которых изображен коврик с вырезанным кругом или прямоугольником. Отдельно необходимо изобразить варианты «заплаток» с характерным узором, среди которых ребенку придется найти подходящий для коврика.
Начинать выполнять задания необходимо с цветовых оттенков коврика. Далее предлагать карточки с простыми узорами ковриков, и по мере развития навыков логического выбора, усложнять задания по образцу теста Равена.
Далее предлагать карточки с простыми узорами ковриков, и по мере развития навыков логического выбора, усложнять задания по образцу теста Равена.
Рисунок 3.
«Починка» коврика развивает одновременно ряд важных аспектов: наглядно-образные представления, мыслительные операции, способность к воссозданию целого.
11. Головоломки
Главная особенность головоломок – их универсальность: вне зависимости от возраста, ситуации и стадии обучения они будут эффективны для развития ребенка. Головоломки относятся к занимательной математике не только потому, что в основе почти любой головоломки лежит некий математический замысел, но и потому, что решение головоломки, по своему духу, близко к решению математических проблем.
Кубик Рубика, змейка Рубика, металлические и деревянные объёмные головоломки увлекут не только детей-дошкольников, но и родителей. Решение головоломок может стать отличным хобби для ребёнка. .
12. Пазлы
Собирая картинку из маленьких разрозненных частей, ребёнок не просто весело проводит время, но и учится систематизировать, анализировать, тренирует способность решать задачу многогранно.
Ведь чтобы правильно собрать пазл, нужно учесть множество факторов — форму фрагмента, последовательность сборки, и, конечно, представлять конечный результат. Начиная с простых пазлов с крупными деталями, дошкольник постепенно перейдёт к наборам с большим количеством уже мелких деталей, а дальше и к 3-D пазлам, что будет способствовать развитию математических способностей.
Как видите, существует огромное количество способов, которые помогут вашему ребёнку понять и усвоить математическую науку. Важно помнить, что ни одно супер-пособие не сделает из ребёнка гения математики, если вы купите его, но не станете заниматься с ребёнком вместе.
Для получения хороших результатов, очень важно, чтобы родители занимались с ребёнком систематически. Играйте в игры, решайте головоломки, считайте машины, птиц, сравнивайте окружающие предметы, отмечайте в календаре дни недели, складывайте камушки, палочки, листочки — и результатом этого станет хорошая успеваемость вашего ребёнка в школе и во взрослой жизни!
5 шагов, как развивать математические способности у ребёнка
Развивать математические способности у дошкольника родитель может самостоятельно. Вот основные шаги, которые помогут малышу с лёгкостью понять мир цифр.
Вот основные шаги, которые помогут малышу с лёгкостью понять мир цифр.
1. Учим ребёнка сравнивать предметы.
Сначала малышу нужно освоить понятия, затем он без проблем сможет их сравнить. Если ребёнок знает, какой смысл спрятан в слове «большой», а что значит «маленький», то сравнить предметы по размеру ему будет несложно. Например: «Смотри
Развитие первых математических представлений у малыша.
Мифы и легенды
- Древняя Греция (4)
- Мифы и легенды (все) (4)
Русские народные сказки
- Волшебные сказки (54)
- Про животных (38)
- Бытовые сказки (22)
- Русские народные сказки (все) (114)
Русские сказочники
- Пляцковский М.С. (46)
- Бианки В.В. (30)
- Абрамцева Н.К. (29)
- Михалков С.В. (28)
- Сутеев В.Г. (27)
- Пермяк Е.А. (26)
- Козлов С.Г. (23)
- Остер Г.
 Б. (21)
Б. (21) - Цыферов Г.М. (17)
- Усачёв А.А. (16)
- Мамин-Сибиряк Д.Н. (15)
- Толстой А.Н. (13)
- Заходер Б.В. (13)
- Прокофьева С.Л. (12)
- Маршак С.Я. (11)
- Берестов В.Д. (11)
- Бажов П.П. (11)
- Иванов А.А. (9)
- Пушкин А.С. (9)
- Коваль Ю.И. (8)
- Успенский Э.Н. (7)
- (7)
- Волков А.М. (6)
- Осеева В.А. (5)
- Одоевский В.Ф. (3)
- Толстой Л.Н. (3)
- Карганова Е.Г. (2)
- Катаев В.П. (2)
- Телешов Н.Д. (2)
- Шварц Е.Л. (2)
- Хармс Д. (2)
- Непомнящая Д. (1)
- Аксаков С.Т. (1)
- Любавина Н.И. (1)
- Ершов П.П. (1)
- Яновский Е. (1)
- Русские сказочники (все) (421)
Сказки народов мира
- Британские сказки (38)
- Арабские сказки (33)
- Украинские сказки (30)
- Прибалтийские сказки (16)
- Немецкие сказки (12)
- Белорусские сказки (11)
- Норвежские сказки (6)
- Шведские сказки (3)
- Сказки народов мира (все) (149)
Зарубежные сказочники
- Ганс Христ.
 Андерсен (47)
Андерсен (47) - Братья Гримм (44)
- Джанни Родари (34)
- Дональд Биссет (33)
- Харрис Д.Ч. (24)
- Шмидт А. (16)
- Киплинг Р. (14)
- Поттер Б. (14)
- Каралийчев А. (13)
- Астрид Линдгрен (12)
- Шарль Перро (11)
- Хогарт Энн (9)
- Оскар Уайльд (9)
- Пройслер О. (8)
- Топелиус С. (8)
- Асбьёрнсен П.К. (5)
- Алан Милн (5)
- Вильгельм Гауф (4)
- Стюарт П. и Риддел К. (4)
- Якобсон А. (3)
- Барри Д.М. (2)
- Валенберг А. (2)
- Лагерлёф С. (2)
- Холабёрд К. (1)
- Распе Р.Э. (1)
- Лилиан Муур (1)
- Балинт А. (1)
- Диккенс Ч. (1)
- Ширнек. Х. (1)
- Бергман Я. (1)
- Вернер Н. (1)
- Зарубежные сказочники (все) (331)
Сказки наших читателей
- Головко А.В. (16)
- Анна Сон (12)
- Малышев М.Н. (11)
- Авдеенко К. (4)
- Скородинская Д. (3)
- Элина (2)
- Полянский В.
 (2)
(2) - Душкина Н.В. (1)
- Вдовиченко И.Г. (1)
- Сказки наших читателей (все) (52)
Организация индивидуальной работы по формированию элементарных математических представлений у детей 4-5 лет
Из опыта работы
«Организация индивидуальной работы по формированию
элементарных математических представлений у детей 4-5 лет»
Парфёнова Светлана Александровна,
Алексеева Ольга Александровна,
воспитатели МАДОУ № 35,
г. Апатиты
Каждый ребёнок имеет свои особенности нервной системы и психофизического развития, а значит, он неповторим. Во все времена российских и зарубежных педагогов волновал вопрос индивидуального подхода к детям. Педагогу необходимо знать основные принципы изучения индивидуальных особенностей для того, чтобы организовать эффективное взаимодействие с детьми, строить стратегию индивидуального развития каждого воспитанника. Спланировать содержание индивидуальной работы воспитателю помогают наблюдение за воспитанниками в повседневной жизни, анализ их поведения и деятельности, беседы с родителями.
Спланировать содержание индивидуальной работы воспитателю помогают наблюдение за воспитанниками в повседневной жизни, анализ их поведения и деятельности, беседы с родителями.
Работая в дошкольном образовательном учреждении, мы стремимся к тому, чтобы наши воспитанники добились высоких результатов в усвоении программных задач, имели познавательную мотивацию, проявляли самостоятельность, активность, инициативу в общении и деятельности. Этого результата невозможно достичь, опираясь только на специально организованную образовательную деятельность. Необходимы индивидуальные занятия.
В октябре этого года мы приступили к работе с новым составом детей. В ходе педагогического наблюдения и проведенного мониторинга заметили, что счетные навыки некоторых воспитанников развиты недостаточно. У других же, наоборот – с опережением программных задач. Именно на этом мы сделали акцент в своей работе. В ходе организованной деятельности уделить должное внимание всем детям очень трудно. И чтобы помочь детям в усвоении программного материала, развить их интерес к занятиям по ФЭМП мы ежедневно проводим индивидуальные занятия с воспитанниками.
И чтобы помочь детям в усвоении программного материала, развить их интерес к занятиям по ФЭМП мы ежедневно проводим индивидуальные занятия с воспитанниками.
Математика — наука фундаментальная…, набор абстрактных форм, математических структур. Как же эту «сухую» науку сделать увлекательной для дошкольников? Конечно, через игру! Ребенок-дошкольник находится во власти эмоциональных проявлений. Обычно приятные эмоции, которые связаны с успехом, повышают эффективность решения различных задач. Активное развитие любознательных качеств в ребенке способствует формированию эмоций, связанных с удивлением и радостью открытий.
Для того, чтобы у ребенка возникало желание выполнить задание, мы подготовили дидактический материал, соответствующий возрасту воспитанников – пособия и игры, многие из низ изготовлены своими руками.
Математическая игра-тренажер «Играй и считай!» представляет собой несколько отдельных игр (счетных полос) от 1 до 5 и от 1 до 10, выполненных из фетра.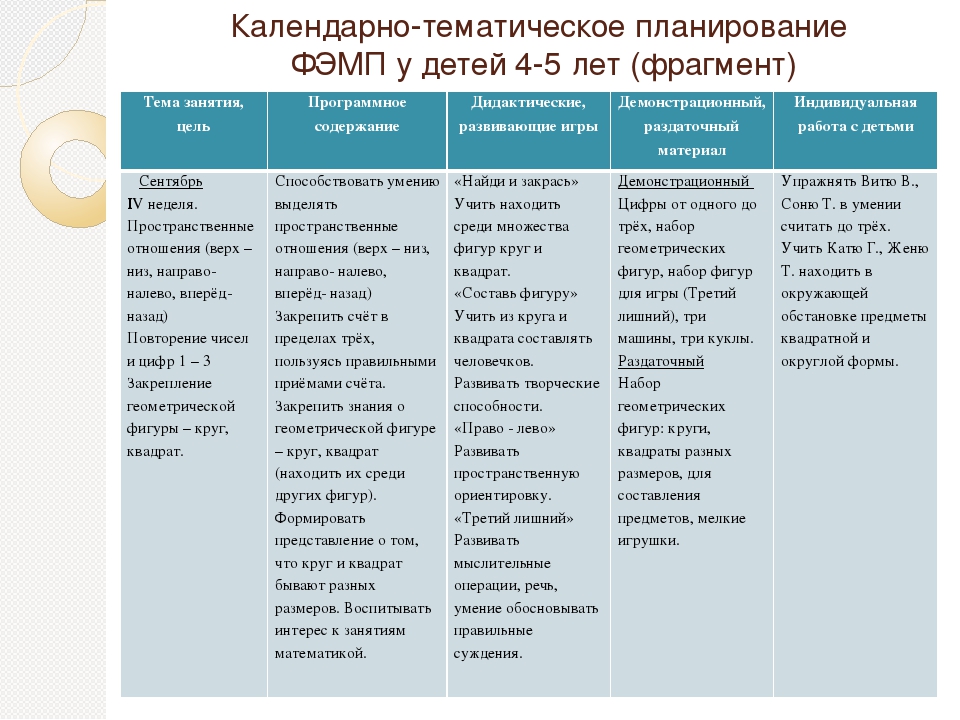 На лицевой стороне изображены картинки (5 или 10 и соответствующая цифра), на оборотной – цифры (от 1 до 4 или от 1 до 9). Во время игры ребенку предлагается посмотреть, кто же будет играть с ним, обследовать фигурки пальчиками. Перевернув игру, знакомим с цифрами, даем возможность так же обследовать их.
На лицевой стороне изображены картинки (5 или 10 и соответствующая цифра), на оборотной – цифры (от 1 до 4 или от 1 до 9). Во время игры ребенку предлагается посмотреть, кто же будет играть с ним, обследовать фигурки пальчиками. Перевернув игру, знакомим с цифрами, даем возможность так же обследовать их.
Цель игры-тренажера: формирование счетных навыков у дошкольников.
Задачи:
- Закреплять знания детей о последовательности чисел в пределах 10.
- Закреплять количественный и порядковый счет (от 1 до 10).
- Формировать умение определять последующее и предыдущее число к заданному.
- Упражнять в прямом и обратном счете в пределах 10.
- Развивать внимание, мышление, мелкую моторику, тактильные ощущения.
- Способствовать развитию интереса к математической деятельности посредством активизации положительных эмоций.
Инструкция к игре-тренажеру «Играй и считай!». Ребенку предлагается посчитать, сколько птичек/рыбок будет играть с ним в прятки. «Смотри, перед нами 5 птичек, а это цифра 5 (показываем). Одна птичка решила спрятаться (заворачиваем край полоски). Спряталась! Посчитай, сколько птичек осталось? А вот и цифра 4 появилась!». Аналогично по очереди прячутся все птички, полоска постепенно сворачивается полностью. Таким образом, закрепляем обратный счет. Затем полоска разворачивается. И птички появляются одна за другой. Для закрепления количественного, порядкового счета спрашиваем: «Сколько птичек будет играть с нами в прятки?», «Какая по счету птичка спряталась?».
«Смотри, перед нами 5 птичек, а это цифра 5 (показываем). Одна птичка решила спрятаться (заворачиваем край полоски). Спряталась! Посчитай, сколько птичек осталось? А вот и цифра 4 появилась!». Аналогично по очереди прячутся все птички, полоска постепенно сворачивается полностью. Таким образом, закрепляем обратный счет. Затем полоска разворачивается. И птички появляются одна за другой. Для закрепления количественного, порядкового счета спрашиваем: «Сколько птичек будет играть с нами в прятки?», «Какая по счету птичка спряталась?».
Используем в своей работе разнообразный подручный материал. Игры с пуговицами, киндер-игрушки, счетные палочки помогают развивать не только счетные навыки, но и ориентировку на плоскости, мелкую моторику.
Авторская игра «Подбери мышке украшение». Игра выполнена из бросового материала: мышки – обвязанные киндер-капсулы, хвост – шнурок, украшения — разноцветные пластиковые крышечки с отверстиями.
Инструкция: «Мышки, собираясь на праздник, украшают свой хвостик бусинами. Мышка в зеленом платье выбрала для себя вот такие бусы (воспитатель показывает ребенку карточку – схему). Помоги мышке нарядиться». Во время игры дошкольники закрепляют навыки счета. Помимо этого, упражняются в работе с карточками – схемами, учатся выполнять задания по образцу, закрепляют основные цвета.
Мышка в зеленом платье выбрала для себя вот такие бусы (воспитатель показывает ребенку карточку – схему). Помоги мышке нарядиться». Во время игры дошкольники закрепляют навыки счета. Помимо этого, упражняются в работе с карточками – схемами, учатся выполнять задания по образцу, закрепляют основные цвета.
Фетровый театр «Три поросенка». Придумывая различные сюжеты, воспитатель предлагает ребятам задания на сравнение групп предметов, способствует усвоению детьми математического понятия «Столько – сколько».
Дети 4-5 лет знают еще не все цифры, называют или узнают лишь некоторые из них. Определенные трудности возникают, когда результат счета надо обозначить цифрой с необходимым количеством предметов. Для решения этой проблемы изготовили цифры из бумаги, картона, фетра, на магнитах. Такие дидактические игры, как «Узнай цифру на ощупь», «Назови имя цифры», «Раскрась цифры» пробуждают в дошкольниках интерес к математической деятельности, в игровой форме помогают сформировать представление о цифрах.
Привлекательный и яркий, побуждающий положительные эмоции, весь дидактический материал в группе находится в полной доступности детям.
Считаем, что индивидуальные занятия с дошкольниками предполагают совместный поиск решения, интеллектуальное сотрудничество со взрослым. Для достижения положительного результата нам помогают такие педагогические приемы, как объяснение, подсказка, поощрение. Нетравмирующая положительная оценка подкрепляет стремление ребенка что-то сделать, узнать.
При работе с неуверенными детьми создаем «ситуацию успеха», предвосхищение ситуации. Накануне занятия мы знакомим их с новым материалом, тем самым повышаем активность ребенка в ходе образовательной деятельности, способствуем развитию чувства уверенности в себе. Самооценка повышается, появляется осознание собственной ценности.
Для детей, идущих с опережением программы, мы предлагаем задания повышенной сложности, ориентируясь на зону ближайшего развития.
Индивидуальная работа с детьми приносит положительные результаты тогда, когда ребята систематически упражняются в счетных навыках в повседневной жизни, а не только на занятиях по математике. Поэтому своим воспитанникам предлагаем разнообразные игровые задания во время прогулок: «Посчитайте, сколько птичек в кормушке?»; «Пять ребят будут кататься с горки, сколько нужно для этого ледянок?». В ходе сюжетно-ролевых игр: «Постройте столько гаражей, сколько машин к вам приехало»; «Постройте домик, в котором будет 3 этажа». Дежурным по столовой необходимо накрыть стол на определенное количество персон и т.д.
Поэтому своим воспитанникам предлагаем разнообразные игровые задания во время прогулок: «Посчитайте, сколько птичек в кормушке?»; «Пять ребят будут кататься с горки, сколько нужно для этого ледянок?». В ходе сюжетно-ролевых игр: «Постройте столько гаражей, сколько машин к вам приехало»; «Постройте домик, в котором будет 3 этажа». Дежурным по столовой необходимо накрыть стол на определенное количество персон и т.д.
Оформляем для родителей воспитанников информационные стенды «Наши достижения ИЛИ Чему мы уже научились», «Что необходимо повторить и закрепить дома». Проводим индивидуальное консультирование родителей, рассказывая об успехах или затруднениях детей, нацеливая на сотрудничество.
Комментирование и размещение ссылок запрещено.
Math Play: Как маленькие дети подходят к математике
Четырехлетняя Нита играет с четырьмя куклами из набора из шести. Проходя мимо, ее учитель спрашивает: «А где остальные?» Ее учитель слышит, как Нита говорит: «Эммм … [указывая на каждую куклу] Я называю тебя« одна ». Вы «два», «три» и «четыре». Где твои сестры, пятерка и шестерка? » Еще минуту она играет с куклами. «О! Тебе шесть? А тебе пять? Ну, пойдем поищем сестер три и четыре». Я тоже должен их найти.«
Проходя мимо, ее учитель спрашивает: «А где остальные?» Ее учитель слышит, как Нита говорит: «Эммм … [указывая на каждую куклу] Я называю тебя« одна ». Вы «два», «три» и «четыре». Где твои сестры, пятерка и шестерка? » Еще минуту она играет с куклами. «О! Тебе шесть? А тебе пять? Ну, пойдем поищем сестер три и четыре». Я тоже должен их найти.«
Нита включила в игру счет, чтобы следить за своими куклами. Мы знаем, что игра важна для развития маленьких детей, поэтому неудивительно, что детская игра является источником их первого «предматематического» опыта.
Изучение математики в игре
Дети интенсивно начинают играть. Преследуя свои собственные цели, они склонны решать проблемы, которые достаточно сложны, чтобы быть увлекательными, но все же не выходят за рамки их возможностей. Сохранение проблемы — разгадывание ее и различные подходы к ней — может привести к эффективному обучению; кроме того, когда несколько детей пытаются решить одну и ту же проблему, они часто придумывают разные подходы, обсуждают разные стратегии и учатся друг у друга. .Эти аспекты игры могут способствовать мышлению и обучению как по математике, так и в других областях.
.Эти аспекты игры могут способствовать мышлению и обучению как по математике, так и в других областях.
Маленькие дети исследуют узоры и формы, сравнивают размеры и считают. Но как часто они это делают? А что это значит для развития детей? Когда детей изучали в свободной игре, возникло шесть категорий содержания математики.
1. Классификация. Одна девушка, Анна, вынула все пластиковые жучки из контейнера и отсортировала их по типу жуков, а затем по цвету.
2. Изучение звездной величины (описание и сравнение размеров объектов). Когда Брианна принесла газету к столу для художников, чтобы накрыть ее, Эми заметила: «Она недостаточно велика, чтобы накрыть стол».
3. Перечисление (произнесение числовых слов, подсчет, мгновенное распознавание ряда объектов или чтение или запись чисел). Три девочки нарисовали свои семьи и обсудили, сколько у них братьев и сестер и сколько лет их братьям и сестрам.
4.Исследование динамики (складывание, разборка или изучение движений, таких как переворачивание). Несколько девушек превратили глиняный шар в диск, разрезали его и сделали «пиццу».
Несколько девушек превратили глиняный шар в диск, разрезали его и сделали «пиццу».
5. Изучение узора и формы (определение или создание узоров или форм или изучение геометрических свойств). Дженни сделала бусы, создав узор желто-красного цвета.
6. Исследование пространственных отношений (описание или рисование местоположения или направления).Когда Тереза поставила диван в кукольном домике у окна, Кэти переместила его в центр гостиной, сказав: «Диван должен быть перед телевизором».
Диапазон математических исследований, изучаемых во время свободной игры, впечатляет. Мы видим, что бесплатная игра предлагает богатую основу для построения интересной математики. Эти повседневные переживания составляют основу более поздней математики. Позже дети развивают эти идеи. Мы называем этот процесс «математизацией». И мы понимаем, что детям нужны как базовые знания, так и конкретные математические задания.
Play не гарантирует математического развития, но предлагает богатые возможности.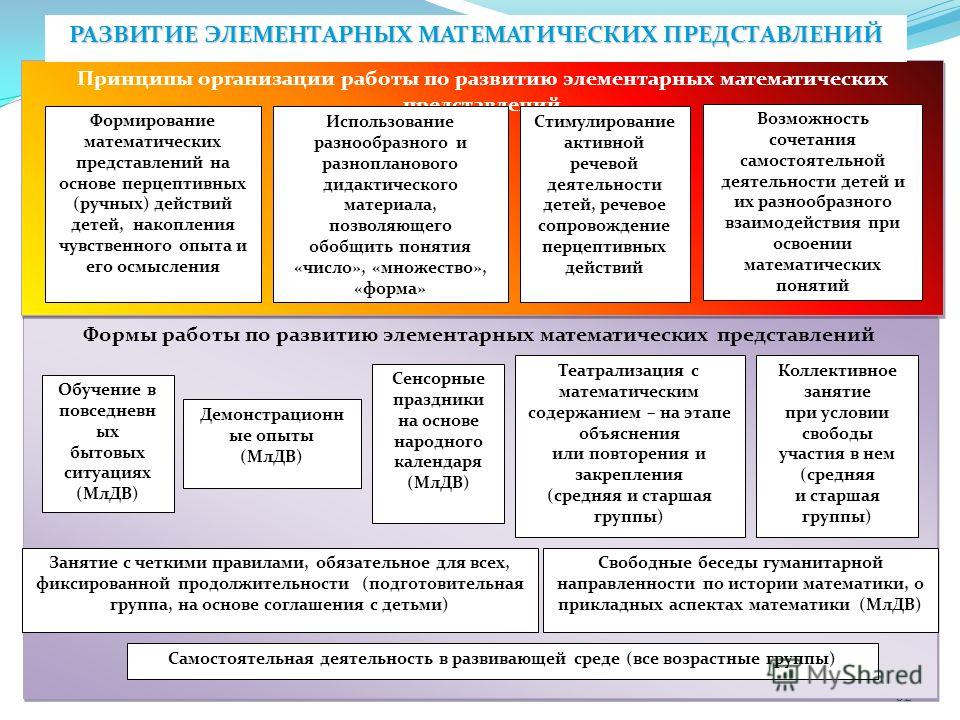 Значительные выгоды будут более вероятными, когда учителя продолжат обучение, вовлекая детей в размышления и представление математических идей, возникших в их игре. Учителя улучшают обучение детей математике, когда они задают вопросы, которые вызывают уточнения, расширения и развитие нового понимания.
Значительные выгоды будут более вероятными, когда учителя продолжат обучение, вовлекая детей в размышления и представление математических идей, возникших в их игре. Учителя улучшают обучение детей математике, когда они задают вопросы, которые вызывают уточнения, расширения и развитие нового понимания.
Математические блоки: башни обучения
Преимущества блочного строительства глубоки и широки.Строя из кубиков, дети развивают свои математические, естественные и общие способности к рассуждению. Рассмотрим, как развивается блочное строительство.
Младенцы мало интересуются штабелированием. Укладка начинается в 1 год, когда младенцы демонстрируют свое понимание пространственных отношений «на». Отношения «следующего за» развиваются примерно через полтора года. В 2 года дети ставят каждый следующий кубик на предыдущий или рядом с ним. Они, кажется, понимают, что блоки не падают при таком размещении.Дети начинают размышлять и предвкушать. В возрасте от 3 до 4 лет дети регулярно строят вертикальные и горизонтальные элементы здания. Когда их просят построить высокую башню, они используют длинные блоки вертикально, потому что, помимо стремления сделать стабильную башню, их цель — сделать стабильную высокую башню, сначала используя только один блок таким образом, а затем несколько. Через 4 года они могут использовать несколько пространственных отношений, расширяя свои здания в нескольких направлениях и с несколькими точками соприкосновения между блоками, демонстрируя гибкость в том, как они строят и интегрируют части конструкции.
Когда их просят построить высокую башню, они используют длинные блоки вертикально, потому что, помимо стремления сделать стабильную башню, их цель — сделать стабильную высокую башню, сначала используя только один блок таким образом, а затем несколько. Через 4 года они могут использовать несколько пространственных отношений, расширяя свои здания в нескольких направлениях и с несколькими точками соприкосновения между блоками, демонстрируя гибкость в том, как они строят и интегрируют части конструкции.
Дошкольники используют, по крайней мере на интуитивном уровне, более сложные геометрические концепции, чем большинство детей испытывают в начальной школе, играя в блоки. Например, один дошкольник, Хосе, кладет двойной блок на коврик, два блока — на блок с двумя блоками и треугольник — в середину, создавая симметричную структуру.
Представьте дошкольника, который строит нижний этаж блочного дома. Он кладет вниз два длинных блока, идущих в одном направлении.Затем он пытается перебросить два конца коротким блоком. Он не достигает, поэтому он перемещает конец одного из длинных блоков, чтобы он достиг. Однако, прежде чем он снова попробует короткий блок, он осторожно настроит другой конец длинного блока. Он пробует короткий блок. Он тянется. Он быстро ставит много коротких блоков, создавая пол своего дома.
Он не достигает, поэтому он перемещает конец одного из длинных блоков, чтобы он достиг. Однако, прежде чем он снова попробует короткий блок, он осторожно настроит другой конец длинного блока. Он пробует короткий блок. Он тянется. Он быстро ставит много коротких блоков, создавая пол своего дома.
Мы многому научились из этого и других подобных эпизодов. Как и этот маленький мальчик, многие дети интуитивно используют понятия параллельности и перпендикулярности.Мальчик даже, кажется, понимает своими действиями, что параллельные линии всегда находятся на одинаковом расстоянии друг от друга!
Мы наблюдали, как другие дети регулируют два цилиндра так, чтобы расстояние между ними было равным длине длинного блока. Они оценивают, сколько еще блоков им нужно, чтобы отделать поверхность. По их оценкам, потребовалось восемь блоков, если каждый квадрат четырех размеров был покрыт двумя блоками. Мы знаем многих учителей математики, которые были бы в восторге, если бы их ученики продемонстрировали такое же понимание геометрии, измерений и чисел!
Ритм и паттерны
Дошкольники также занимаются ритмическими и музыкальными паттернами. Они могут добавлять в свой репертуар более сложные, продуманные паттерны, такие как «хлопок, хлопок, пощечина; хлопок, хлопок, пощечина». Они могут говорить об этих узорах, представляя узор словами. Детсадовцам нравится придумывать новые движения, чтобы соответствовать одному и тому же шаблону, поэтому хлопок, хлопок пощечину трансформируется в прыжок, прыжок, падение; прыгать, прыгать, падать и скоро символизируется шаблоном AABAAB. Воспитанники детского сада также могут описывать такие узоры цифрами («два чего-то, потом один чего-то другого»). На самом деле это первые четкие связи между шаблонами, числами и алгеброй.
Они могут добавлять в свой репертуар более сложные, продуманные паттерны, такие как «хлопок, хлопок, пощечина; хлопок, хлопок, пощечина». Они могут говорить об этих узорах, представляя узор словами. Детсадовцам нравится придумывать новые движения, чтобы соответствовать одному и тому же шаблону, поэтому хлопок, хлопок пощечину трансформируется в прыжок, прыжок, падение; прыгать, прыгать, падать и скоро символизируется шаблоном AABAAB. Воспитанники детского сада также могут описывать такие узоры цифрами («два чего-то, потом один чего-то другого»). На самом деле это первые четкие связи между шаблонами, числами и алгеброй.
Дети, которые испытали эти ритмические переживания, намеренно воссоздают и обсуждают шаблоны в своих произведениях искусства. Один четырехлетний ребенок любил знать цвета радуги (ROY G BFV, красный, оранжевый, желтый, зеленый, синий, индиго, фиолетовый) и рисовал радуги, цветы и рисунки, повторяющие эту последовательность несколько раз.
Математика течет сквозь воду Играть
Измерение часто лежит в основе игры в воде или на песчаном столе. Исследователь рассказывает о посещении двух классных комнат в один день и наблюдении за игрой в воде в обоих.Дети наливали воду в каждую комнату, но в одной они также возбужденно наполняли одну и ту же чашку в разные емкости, считая, сколько чашек они могли «уместить» в каждую емкость. Единственная разница между этими двумя классами заключалась в том, что в последнем учитель прошел мимо и небрежно спросил: «Интересно, в каком из них больше всего чашек воды?»
Исследователь рассказывает о посещении двух классных комнат в один день и наблюдении за игрой в воде в обоих.Дети наливали воду в каждую комнату, но в одной они также возбужденно наполняли одну и ту же чашку в разные емкости, считая, сколько чашек они могли «уместить» в каждую емкость. Единственная разница между этими двумя классами заключалась в том, что в последнем учитель прошел мимо и небрежно спросил: «Интересно, в каком из них больше всего чашек воды?»
Развертывание математических концепций!
Такие материалы, как песок и пластилин, открывают множество возможностей для математического мышления и рассуждений.Учителя могут предоставить полезные материалы (формочки для печенья), параллельно играть с детьми и задавать вопросы или комментарии относительно форм и количества предметов. Например, они могут сделать несколько копий одной и той же формы в пластилине с помощью форм для печенья или превратить песок или пластилин в разные объекты. Одна учительница сказала двум мальчикам, что собирается «спрятать» шар пластилина, накрыв его плоским предметом и надавив на него. Мальчики сказали, что мяч все еще на месте, но когда она подняла его, мяч «исчез».«Это их обрадовало, они скопировали ее действия и обсудили, что мяч находится« в »плоской части.
Мальчики сказали, что мяч все еще на месте, но когда она подняла его, мяч «исчез».«Это их обрадовало, они скопировали ее действия и обсудили, что мяч находится« в »плоской части.
Математика и манипуляции
Детские игры с манипуляторами, в том числе объединение «плоских» блоков для создания картинок и рисунков, а также для решения головоломок, показывают прогресс в развитии, как и построение блоков. Дети сначала не умеют сочетать формы. Постепенно они учатся видеть как отдельные части, так и «целое», и узнают, что части могут составлять целое и при этом оставаться частями.Примерно к 4 годам большинство из них может решать головоломки методом проб и ошибок и создавать картинки с фигурами, расположенными рядом друг с другом. С опытом они постепенно учатся комбинировать формы, чтобы создавать более крупные формы. Они становятся все более преднамеренными, создавая мысленные образы форм и их атрибутов, таких как длина сторон и углы.
Создание концепций с помощью компьютеров
Создание рисунков с фигурами можно выполнять с помощью строительных блоков, а также компьютерных фигур. Компьютерные версии имеют то преимущество, что они дают немедленную обратную связь.Например, фигуры могут быть прозрачными, чтобы дети могли видеть загадку под ними. Кроме того, дети часто больше говорят и больше объясняют, что они делают на компьютере, чем при использовании других материалов. На более высоких уровнях компьютеры позволяют детям разбивать и складывать фигуры способами, невозможными с помощью физических блоков.
Компьютерные версии имеют то преимущество, что они дают немедленную обратную связь.Например, фигуры могут быть прозрачными, чтобы дети могли видеть загадку под ними. Кроме того, дети часто больше говорят и больше объясняют, что они делают на компьютере, чем при использовании других материалов. На более высоких уровнях компьютеры позволяют детям разбивать и складывать фигуры способами, невозможными с помощью физических блоков.
Компьютеры также могут облегчить игру. Добавление компьютерного центра не нарушает текущую игру, но облегчает позитивное социальное взаимодействие и сотрудничество.Исследования показывают, что компьютерная деятельность более эффективна в стимулировании вокализации, чем игра с игрушками, а также стимулирует более высокий уровень социальной игры. Кроме того, совместная игра за компьютером похожа на совместную игру в центре блока. Сотрудничество в компьютерном центре может обеспечить контекст для инициирования и поддержания взаимодействия, которое может быть перенесено и на игры в других областях, особенно для мальчиков.
Драматическая математика
Драматическая игра может быть естественной математической при правильной настройке.В одном исследовании учителя и дети организовали магазин в зоне драматических игр, где продавец заполняет заказы и просит у покупателя деньги (1 доллар за каждую игрушку динозавра).
В одном классе Габи работала продавцом. Тамика вручила ей пять карточек (5 точек и цифра «5») в качестве ее приказа. Габи отсчитала пять игрушечных динозавров.
Учитель (только входящий в зону): Сколько вы купили?
Тамика: Пять.
Учитель: Откуда ты знаешь?
Тамика: Потому что Габи посчитала.(Тамика все еще работала над своими счетными навыками и доверяла счету Габи больше, чем ее собственному знанию пяти. Игра позволила ей развить свои знания.)
Жанель: Я получаю большой номер. (Она протянула Габи карты 2 и 5.)
Габи: У меня не так много.
Учитель: Вы можете дать Жанель 2 одного вида и 5 другого.
Когда Габи отсчитала две отдельные стопки и положила их в корзину, Джанель отсчитала доллары.Она неправильно посчитала и дала ей 6 долларов.
Габи: Вам нужно 7 долларов.
Эта театрально-игровая постановка с помощью учителя «работала» для детей с разным уровнем математического мышления.
Играйте перед решением проблем
Мы видели, как различные виды игр улучшают математическое мышление детей. Исследования также показывают, что если дети играют с объектами до того, как их попросят решить с ними проблемы, они добиваются большего успеха и творчески.Например, в одном исследовании с тремя группами детей от 3 до 5 лет их попросили достать предмет с помощью коротких палок и соединителей. Одной группе было разрешено поиграть с палками и соединительными устройствами, одну группу научили, как можно соединять палки, а одну группу попросили выполнить задание без предварительной игры или обучения. Первые две группы показали одинаковые результаты и достигли лучших результатов, чем третья группа. Часто группа, которая просто играла с клюшками и соединителями, сначала решала проблему быстрее, чем группа, которую учили их использовать.
Часто группа, которая просто играла с клюшками и соединителями, сначала решала проблему быстрее, чем группа, которую учили их использовать.
Математическая игра
Это подводит нас к заключительному захватывающему и обычно упускаемому из виду типу игры: математической игре. Здесь мы не имеем в виду игру, включающую математику — мы говорили об этом на протяжении всей статьи. Мы имеем в виду игру с самой математикой.
Подумайте еще раз о Ните и ее куклах. Когда она назвала их, чтобы идентифицировать «сестер», с которыми она не играла, она использовала математику в своей игре. Но когда она решила, что переименует куклы, которые у нее были с собой, с «пять» и «шесть» на «три» и «четыре», она играла с понятием, что присвоение номеров коллекции объектов произвольно.Еще она считала не только куклы, но и сами счетные слова. Она сосчитала слова «три, четыре» и увидела, что пропали две сестры. Она играла с идеей, что подсчет слов можно считать.
Динамические аспекты компьютеров часто вовлекают детей в математические игры больше, чем физические манипуляции или бумажные материалы. Например, два дошкольника играли с заданиями под названием «Время вечеринки» из проекта «Строительные блоки», в котором они могли выставить любое количество предметов, а компьютер их подсчитывал и маркировал.»У меня есть мысль!» — сказала одна девушка, убирая все предметы и перетаскивая салфетки на каждый стул. «Вы должны поставить чашки для всех. Но сначала вы должны сказать мне, сколько чашек это будет». Прежде чем ее подруга начала считать, она прервала: «И всем нужна одна чашка молока и одна чашка сока!» Девочки сначала усердно работали вместе, пытаясь найти чашки в центре драматургии, но, наконец, сосчитали по два раза на каждой подставке для столовых приборов на экране. Их ответ — изначально 19 — не был точным, но они не расстроились, когда их исправили, когда они на самом деле поставили чашки и обнаружили, что им нужно 20.Эти дети играли с математикой ситуации, с решениями, играя вместе друг с другом.
Например, два дошкольника играли с заданиями под названием «Время вечеринки» из проекта «Строительные блоки», в котором они могли выставить любое количество предметов, а компьютер их подсчитывал и маркировал.»У меня есть мысль!» — сказала одна девушка, убирая все предметы и перетаскивая салфетки на каждый стул. «Вы должны поставить чашки для всех. Но сначала вы должны сказать мне, сколько чашек это будет». Прежде чем ее подруга начала считать, она прервала: «И всем нужна одна чашка молока и одна чашка сока!» Девочки сначала усердно работали вместе, пытаясь найти чашки в центре драматургии, но, наконец, сосчитали по два раза на каждой подставке для столовых приборов на экране. Их ответ — изначально 19 — не был точным, но они не расстроились, когда их исправили, когда они на самом деле поставили чашки и обнаружили, что им нужно 20.Эти дети играли с математикой ситуации, с решениями, играя вместе друг с другом.
Математика может быть интересна детям по сути, если они строят идеи во время математической игры.
Развитие математики в повседневной игре
Учителя поддерживают математику в игре, создавая благоприятную среду и надлежащим образом вмешиваясь. Вот что вы можете сделать:
Понаблюдайте за детской игрой. Если вы не видели много новых блочных конструкций, поделитесь книгами, иллюстрирующими различное расположение блоков, или разместите изображения в центре блока.Когда вы видите, как дети сравнивают размеры, предлагайте разные предметы, которые дети могут использовать для измерения своих структур, от кубиков до ниток и линейок.
Вступайте чутко. Полезная стратегия — спросить, развиваются ли социальное взаимодействие и математическое мышление или застопорились. Если они развиваются, просто понаблюдайте и оставьте детей в покое. Обсудите этот опыт позже со всем классом.
Обсудить и уточнить идеи. Каждый из детей может утверждать, что их блочное здание больше.Вы можете видеть, что один ребенок говорит о высоте, а другой — о ширине. Вы можете по-разному прокомментировать, как вы видите здания такими большими, как в примере «У вас очень высокое здание, а здание Криса кажется очень широким».
Вы можете по-разному прокомментировать, как вы видите здания такими большими, как в примере «У вас очень высокое здание, а здание Криса кажется очень широким».
Запланируйте длинные отрезки времени для игры. Обеспечивает улучшенную среду и материалы, в том числе структурированные материалы, такие как блоки и лего, которые стимулируют математическое мышление.
Дети младшего возраста активно используют математическое мышление и рассуждения в своей игре, особенно если они обладают достаточными знаниями об используемых материалах, если задача понятна и мотивирует, а контекст знаком и удобен.Математику можно легко интегрировать в текущую игру и деятельность детей, но для этого требуется знающий учитель, который создает благоприятную среду и предлагает соответствующие задачи, предложения, задания и язык. В классах, где учителя внимательны ко всем этим возможностям, детские игры обогащают математические исследования.
Ресурсы для учителей: веб-сайты
Самая важная роль учителей в отношении математики должна заключаться в нахождении частых возможностей помочь детям размышлять и расширять математику, возникающую в их повседневной деятельности, беседах и играх, а также в создании среды, поддерживающей такую деятельность.
1. Из NAEYC, статья, показывающая, как можно разрабатывать математические игры на основе детской литературы. NAEYC также предлагает «Математика для детей младшего возраста: содействие хорошему началу», совместное заявление Национальной ассоциации по образованию детей младшего возраста (NAEYC) и Национального совета учителей математики (NCTM).
2. Из Building Blocks (Национальный научный фонд), идеи по поиску математики и развитию математики с помощью детских занятий.
3. Национальный совет учителей математики (NCTM) предлагает математические стандарты, Принципы и стандарты школьной математики, а также множество мероприятий, программные среды на базе Интернета и видеоролики. «Уголок учителей» NCTM предоставляет информацию о возможностях профессионального развития, ресурсах и многом другом.
4. Центр развития учителей «Математические перспективы» предоставляет преподавателям математики дошкольного и шестого классов инструменты, стратегии и оценки, которые гарантируют, что все учащиеся добьются успеха в изучении математики и смогут использовать математику для решения задач, а также математического мышления .
Метод формирования элементарных математических представлений (ФЭМП) в средней группе
Именно в первые годы жизни у ребенка появляется возможность узнать много важной информации. Существует специальная методика формирования элементарных математических представлений, благодаря которой маленький человек получает навыки логического мышления.
Особенности психолого-педагогического исследования
Диагностика, неоднократно проводимая в дошкольных учреждениях, подтверждает возможность формирования основ математического мышления в возрасте 4-7 лет.Эта информация, огромная часть которой приходится на ребенка, предполагает поиск ответов с помощью логических навыков. Различные ролевые игры по ФЭМП в средней группе учат дошкольников воспринимать предметы, сравнивать и обобщать наблюдаемые явления, понимать простейшие взаимосвязи между ними. Основным источником знаний в этом возрасте является интеллектуальный и чувственный опыт. Ребенку сложно правильно выстраивать логические цепочки, поэтому ведущая роль в формировании мышления принадлежит учителю. Любое занятие по ФЭМП в средней группе направлено на развитие детей, подготовку к школе. Современные реалии требуют от репетитора применения основ развивающего обучения, активного использования новаторских методов и методов развития основ математического мышления.
Любое занятие по ФЭМП в средней группе направлено на развитие детей, подготовку к школе. Современные реалии требуют от репетитора применения основ развивающего обучения, активного использования новаторских методов и методов развития основ математического мышления.
История появления ФЭМП в дошкольном образовании
Современный метод формирования простейших математических умений у дошкольников, долгий исторический путь. Впервые вопрос о методах и содержании дошкольного образования по арифметике рассматривался в 17-18 вв. Зарубежными и отечественными педагогами и психологами.В своих образовательных системах, рассчитанных на детей 4-6 лет, К.Д. Ушинский, И.Г. Песталоцци, Я. А. Каменский указал на важность формирования четкого представления о пространстве, мерах измерения различных величин, размеров предметов и предложил алгоритм действий.
Дети дошкольного возраста, учитывая особенности физического и умственного развития, проявляют неустойчивый интерес к следующим математическим понятиям: время, форма, количество, пространство. Им сложно соотнести эти категории друг с другом, упорядочить их, применить полученные знания к конкретным жизненным ситуациям.Согласно новым федеральным образовательным стандартам, разработанным для детских садов, ФЭМП в средней группе является обязательным элементом.
Им сложно соотнести эти категории друг с другом, упорядочить их, применить полученные знания к конкретным жизненным ситуациям.Согласно новым федеральным образовательным стандартам, разработанным для детских садов, ФЭМП в средней группе является обязательным элементом.
В концепции дошкольного образования есть четкие требования к формированию познавательного интереса у будущих первоклассников, частью которого является именно математическое образование.
Значение математических представлений для дошкольников
Обучение детей основам такого рода
Методика формирования элементарных математических представлений (ФЭМП) в средней группе
В первые годы жизни ребенок имеет способность усваивать огромное количество важной информации.Существует особая методика формирования элементарных математических понятий, с помощью которой человечек приобретает навыки логического мышления.
Особенности психолого-педагогического обучения
Диагностика, неоднократно проводимая в государственных дошкольных учреждениях, подтверждает возможность формирования у 4-7 летнего возраста основ математического мышления. Информация в огромном объеме ложится на ребенка, предполагает поиск ответов с применением логических навыков. Разнообразные ролевые ФАН в средней группе учат дошкольников воспринимать предметы, сравнивать и обобщать наблюдаемые явления и понимать элементарные взаимодействия между ними.Основным источником знаний в эту эпоху является интеллектуальный и чувственный опыт. Ребенку сложно самостоятельно выстроить логическую цепочку, поэтому ведущая роль в формировании мышления принадлежит учителю. Любая деятельность в ФЭМП в средней группе направлена на развитие детей, готовящихся к школе. Современные реалии требуют от учителя применения основ развивающего обучения, активного использования новаторских приемов и методов в развитии основ математического мышления.
Информация в огромном объеме ложится на ребенка, предполагает поиск ответов с применением логических навыков. Разнообразные ролевые ФАН в средней группе учат дошкольников воспринимать предметы, сравнивать и обобщать наблюдаемые явления и понимать элементарные взаимодействия между ними.Основным источником знаний в эту эпоху является интеллектуальный и чувственный опыт. Ребенку сложно самостоятельно выстроить логическую цепочку, поэтому ведущая роль в формировании мышления принадлежит учителю. Любая деятельность в ФЭМП в средней группе направлена на развитие детей, готовящихся к школе. Современные реалии требуют от учителя применения основ развивающего обучения, активного использования новаторских приемов и методов в развитии основ математического мышления.
История возникновения ЭКО в дошкольном образовании
Современные методы формирования элементарных математических навыков у детей дошкольного возраста, долгий исторический путь. Вопрос о методах и содержании арифметики дошкольного обучения рассматривался российскими и зарубежными педагогами и психологами XVII – XVIII вв. В своих образовательных системах, рассчитанных на детей 4-6 лет им. К.Д. Ушинского, И.Г. Песталоцци, Я.А. Каменский указали на важность формирования четкого представления о пространстве, измерениях разного количества, размеров предметов, предложили алгоритм действия.
В своих образовательных системах, рассчитанных на детей 4-6 лет им. К.Д. Ушинского, И.Г. Песталоцци, Я.А. Каменский указали на важность формирования четкого представления о пространстве, измерениях разного количества, размеров предметов, предложили алгоритм действия.
Дети дошкольного возраста, особенно с учетом физического и умственного развития, проявляют неустойчивый интерес к следующим математическим понятиям: время, форма, число, пространство. Эти категории сложно связать друг с другом, систематизировать, применить полученные знания к конкретным жизненным ситуациям. Согласно новым Федеральным образовательным стандартам, разработанным для детского сада, ФАН в средней группе является обязательным элементом.
Рекомендуется
Ребенок в 8 месяцев: режим дня.Есть ребенка в 8 месяцев
Вашему ребенку, наконец, восемь месяцев? Как любящий и заботливый родитель, вам просто нужно знать, каким должен быть сейчас режим дня ребенка и как часто вам нужно есть ребенка в этом возрасте. Натуральный рацион ребенка в 8 месяцев отличается от искусственного …
Натуральный рацион ребенка в 8 месяцев отличается от искусственного …
Капсулы для стирки: инструкция по применению и отзывы
Сегодня капсулы для стирки пользуются большим спросом и популярностью. Это потому, что они проявили себя в процессе. Даже самые грязные вещи, сшитые из разных тканей, после первой стирки становятся идеально чистыми.Такого результата невозможно достичь при использовании …
В концепции дошкольного образования наглядно показаны требования к формированию познавательного интереса у будущих первоклассников, и частью его является именно математическое образование.
Значение математических понятий для дошкольников
Обучению детей основам такой сложной науки, как математика, в современном образовании отводится важное место. Такой интерес вызван несколькими причинами:
- Зачисление начинается с 6-7 лет;
- Огромный объем информации требует от ребенка навыков логического мышления;
- Внедрение в учебный процесс информационных технологий (ИКТ).

Особенности дошкольных программ по математике
Ее основным направлением является формирование логических способностей и представлений, стимулирование умственной деятельности, развитие интеллекта дошкольников. Любая деятельность на ФЭМП в средней группе направлена на развитие простейших суждений, развитие грамматически правильной речи.
Математическая подготовка будущих студентов, предусмотренная программой, в дополнение к обучению детей навыкам счета, развитию представлений о числе и количестве первых десяти.ФАН в средней группе предполагает разделение объектов на равные части, измерение объекта с условными измерениями, определение объема твердых и жидких тел. Ребята при выполнении заданий, предложенных учителем, развивают зрение, получают представление о разнообразных геометрических фигурах, формируют представления о пространственных взаимодействиях.
На уроках математики учитель реализует не только основные образовательные цели ФЭМП, в средней группе реализуется образовательная функция. Преподаватель знакомит учеников с правилами поведения, формирует в них дисциплину, трудолюбие, самодисциплину. Работать над формированием у малышей простейших математических понятий учитель ведет в утреннее, дневное, вечернее время 2-3 раза в неделю. ФАН в средней группе ГЭФ помогает учителю развивать в своих подопечных активную гражданственность, целеустремленность, настойчивость и сдержанность.
Преподаватель знакомит учеников с правилами поведения, формирует в них дисциплину, трудолюбие, самодисциплину. Работать над формированием у малышей простейших математических понятий учитель ведет в утреннее, дневное, вечернее время 2-3 раза в неделю. ФАН в средней группе ГЭФ помогает учителю развивать в своих подопечных активную гражданственность, целеустремленность, настойчивость и сдержанность.
Закрепление логических навыков лепки, рисования. Дизайн деталей из бумаги (оригами) способствует закреплению знаний о геометрических фигурах, размерах, количестве предметов.Приложение помогает развить пространственные представления, отработанные на этих занятиях такие качества дошкольников, как пунктуальность, настойчивость. Уроки спорта и музыки включают элементы игры. Математика незаменима во время зарядки, физических упражнений. Подвижные игры, которые учитель использует для закрепления начальных математических концепций, изученных в классе. Летом ФАН средней группы находится в стадии пеших прогулок.
Основные методики ФАН
В качестве основы для обучения математическим умениям дошкольников применялись дидактические методы: последовательность, последовательность, индивидуальность, последовательность.Знания, которые педагог передает малышам от урока к уроку, усложняются с учетом уровня развития детей. Для повтора применяется специальная ролевая игра. Математика попадает в излюбленный предмет дошкольников, они с удовольствием выполнят работу учителя, выискивая сходство и различие в предметах, но ориентируясь на мелкие детали, чтобы найти ответ на свой вопрос.
Развивающее образование
Исследования показывают, что учителя используют разные методы обучения: ясность, игровые технологии: словесные разговоры, мобильные игры, перед опросами.
Особое место в дошкольном математическом образовании занимает педагогическая подготовка. Любой синопсис ФАН в средней группе предполагает использование визуальных средств СПИДа (руководства, справочники, рисунки, фотографии), чтобы дети получали полное представление об объектах, их свойствах и характеристиках.
Требования к иллюстративному материалу в ДОУ
В зависимости от образовательных целей, индивидуальных и возрастных особенностей детей, существуют определенные правила, которые должны полностью соответствовать наглядному математическому материалу:
- Разнообразие размеров, цвета, формы;
- Возможность использования ролевых игр;
- Ловкость, сила, стойкость;
- Эстетические характеристики;
E.В. Сербина в своей книге предлагает «педагогические заповеди», которые использует в работе воспитателя дошкольного учреждения:
- «Не торопиться с результатом». Каждый ребенок развивается по своему «сценарию», важно направлять его, а не пытаться ускорить желаемый результат.
- «Воодушевлять — лучший способ добиться успеха». NOD в FAN в средней группе предполагает поощрение любых усилий ребенка. Учитель должен найти то, за что вы можете поощрить своего ребенка. Ситуацию спешки, которую я создал каждому ученику, способствует развитию логических навыков, повышению интереса к математике.

Особенности работы с дошкольниками
Дошкольный возраст не предполагает использования негативных маркеров, порицания со стороны воспитателя. Нельзя сравнивать достижения одного малыша с результатами другого воспитанника, допускается только анализ индивидуального роста дошкольника. Учитель должен использовать методы и приемы, вызывающие неподдельный интерес его команды. Занятия «принудительно» не принесут пользы, напротив, приведут к формированию отрицательного отношения к математике, вычислительным навыкам.При личном контакте и дружеских отношениях между ребенком и его наставником гарантирован положительный результат.
Разделы дошкольного математического образования
В дошкольном математическом образовании следующие разделы: размер, число, геометрическая форма, ориентация в пространстве во времени. За четыре года студенты осваивают навыки счета, использования чисел, устного выполнения простых вычислительных операций. В этот период вы можете играть в игры с кубиками разного размера, цвета, формы.
В процессе игры воспитатель развивает у детей следующие умения:
- Оперирование свойствами, числами, предметами, обнаружение простых изменений формы, размеров;
- Сравнение, обобщение групп объектов, сопоставление, выявление шаблонов;
- Самостоятельность, выдвижение гипотез, поиск плана действий
Заключение
ГЭФ для дошкольного образования содержит перечень понятий, которые необходимо сформировать у выпускников детских садов.Будущим первоклассникам необходимо знать форму предметов, конструктивные элементы различной геометрической формы, размеры тел, чтобы сравнивать две геометрии, 6-7-летний ребенок использует речь и познавательные навыки. Методы исследования и проектирования помогают развить в детях любознательность. Педагог в развитии математической деятельности подбирает такие формы и методы работы, которые способствовали бы всестороннему развитию дошкольников. В детском саду на первом месте не содержание уроков, а формирование будущего ученика.
Занятия по развитию логики и математики для 2-х летних
Математическое развитие 2-летних детей означает качественные изменения в их познавательной деятельности в результате формирования элементарных математических представлений и понимания несложных логических операций. Математическое развитие — важная составляющая в формировании «картины мира» ребенка.
Различные дидактические игры и задания помогают развить первые математические навыки.Во время игр малыш приобретает новые знания и навыки. Математические занятия способствуют развитию восприятия, внимания, памяти, мышления и творческих способностей. Они способствуют когнитивному развитию в целом.
В начальной школе курс математики не прост. Часто дети испытывают разного рода трудности в математике, потому что они не готовы воспринимать математику как предмет.
Следовательно, родители должны развивать у ребенка интерес к математике с ранних лет.Введение в предмет в игровой и увлекательной форме поможет ребенку быстрее и легче освоить школьную программу в будущем.
Какие математические навыки должен освоить двухлетний ребенок?
- Знать понятие «много — мало».
- Ближе к трем годам — осваивать понятие «больше-меньше».
- Научитесь различать количество предметов: «один» и «два» минимум. Вы можете пойти дальше и научить малыша считать предметы до 5 или до 10, но не все дети в возрасте от 2 до 3 лет интересуются и умеют считать — это нормально.Я имею в виду не просто называть числа от 1 до 10, а считать реальные предметы и понимать значение чисел. Узнайте, как научить ребенка считать.
- Научитесь сортировать объекты по размеру, цвету и типу. Вы можете сортировать разные виды макарон, пуговиц, больших и маленьких предметов, кружков, квадратов и т. Д. Вы можете попробовать другие виды сортировки.
- Научитесь ориентироваться в пространстве (чтобы изучить концепции сверху, снизу, понять правое и левое — вот некоторые упражнения для обучения левому и правому).
- Решать простые головоломки из 2−4 частей без посторонней помощи.
 Эта способность развивается постепенно. Вначале вы должны помочь своему ребенку.
Эта способность развивается постепенно. Вначале вы должны помочь своему ребенку. - Чтобы научиться соответствовать. Спектакль «Кто что ест?», «Чей это дом», «Чей это хвост», «Чей это ребенок»? Используйте специальные наборы карточек или картинок. Я использую такие пазлы:
Я использую такие пазлы:
- Разберись в описании. Мать описывает в простейшей форме предмет или животное, а ребенок отгадывает.Например: «Маленькая, с длинными белыми ушками, прыгает и морковь ест, кто это?» или «Кто говорит« Му-Му »и дает молоко? Можно постепенно усложнять загадки.
- Размещение объектов друг в друге в соответствии с их размером. Вы можете использовать набор матрешек или просто разные чашки или контейнеры для еды.
- Постройте башню из блоков разных размеров. Самый большой должен быть внизу, а самый маленький — вверху.
- Научитесь сопоставлять формы и геометрические тела с их проекциями.Можно использовать специальные блоки Денеш. Они идут с картинками, на которых нужно разместить блоки нужного размера и цвета, чтобы получился рисунок.
Надеюсь, вам понравятся эти математические задания для двухлетних детей, вам также могут понравиться некоторые математические игры.
Математические игры для 2-летних.
Игра помогает развить навыки счета и понять смысл процесса счета.
Необходимое оборудование: плотный цветной картон, ножницы, нитки, пуговицы.
Вырежьте картонное дерево и несколько яблок.Пришейте к веточкам маленькие пуговицы, а к яблокам прикрепите петли. Попросите малыша прикрепить к веткам 2 яблока, а затем пусть «собирает» яблоки. Затем попросите ребенка прикрутить 3 яблока и т. Д.
В игре есть возможность упорядочивать предметы по определенным параметрам.
Необходимое оборудование: 4 бумажных кружка диаметром 3 см и 4 кружка диаметром 6 см. Коробка большая и маленькая.
Придумайте сюжет для вашей игры. Например, ваша бабушка испекла блины — большие и маленькие.Больше — для мамы и папы, а поменьше — для внуков. Но блины испортились. Вам нужно помочь бабушке разложить блины по тарелкам.
Игры и занятия по развитию логики на 2 -3 года.
А как насчет логики? Это важно для 2-летнего ребенка? Да, это! И в этом возрасте логическая и математическая деятельность в основном совпадает, так как ребенок просто не может решать чисто математические задачи. Итак, вот еще несколько занятий для развития логического мышления у малышей.
1. Ближе к трем годам — конструирование несложных конструкций по рисунку (как на картинке, но лучше начать с двух частей и… обратите внимание на цвет!).
2. С 2,5 лет можно играть в Никитин квадрат. Сначала вы будете помогать ребенку складывать кусочки разного цвета в квадраты, но очень быстро он научится делать это без вашей помощи.
3. Научите классифицировать предметы по общей теме. Например: дайте ребенку карточки с изображениями игрушек, еды и животных.Малыш должен разделить их на соответствующие группы. Пусть он положит игрушки в коробку, еду в холодильник, а животных в их импровизированный домик. Сначала ребенок учится классифицировать предметы с вашей активной помощью. Сначала начните с двух наборов карточек — игрушек и еды, затем добавьте третий набор. Когда ваш ребенок освоит эти карты, лучше не добавлять набор 4 и , а начать заново с двумя новыми наборами.
4. Игра с кубиками Денеши или другими подходящими предметами (игрушки, пуговицы, бусинки и т. Д.)):
- найти предметы, фигурки одинаковой формы;
- найти предметы, фигуры одного цвета;
- найти предметы одинакового размера;
5. Идентификация объектов по двум атрибутам (найдите большой желтый кружок, маленький красный квадрат и т. Д.).
6. Ближе к трем годам — найти ошибки в картинках, чего не хватает, что не так, какой неправильный цвет и т.д.
Вы также можете использовать эти картинки с ошибками для развития критического мышления .
Это подсказка! Если ваш ребенок отказывается выполнять какие-то задания или не хочет долго «учиться», не настаивайте. Сделайте всего 1-2 упражнения. Известно, что многие дети до 3 лет не могут долго заниматься чем-то, особенно если им это неинтересно. В другой день у вас будет много времени. Возможно, в следующий раз наш малыш сделает больше.
Наблюдайте внимательно, чтобы ваш ребенок не скучал и не уставал. Старайтесь заниматься образовательной деятельностью не дольше, а чаще. В этом возрасте одно «занятие» должно длиться не более 20 минут для самых усидчивых малышей.Если ваш малыш немного беспокойный, пусть это будет 10-минутный урок. Помните, ежедневное обучение должно приносить ребенку только положительные эмоции.
Изучение математики для двухлетних детей очень важно! Помогите своему ребенку развить математические навыки в раннем возрасте!
Ван де Валле и Бэй-Вильямс, математика в начальной и средней школе: развивающее обучение
- Тематический каталог
- Гуманитарные и социальные науки
- Антропология
- Изобразительное искусство
- Каталог коммуникаций, кино и театра
- Массовые коммуникации / Связи с общественностью / Фильм
- Речевое общение
- Театр
- английский
- Сочинение
- Развивающий английский
- Литература и творческое письмо
- Техническая коммуникация
- История
- Междисциплинарные исследования
- Семейные исследования и человеческое развитие
- Гуманитарные науки
- Расовые и этнические исследования
- Социальная наука
- Женские и гендерные исследования
- Музыка
- Философия
- Политическая наука
- Психология
- Религия
- Социальная работа / семейная терапия / социальные услуги
- Социология
- Мировые языки
- китайский язык
- французкий язык
- Немецкий
- Итальянский
- Японский
- Языковые методы
- латинский
- португальский
- русский
- испанский
- Математика и наука
- Анатомия и физиология
- Биология и микробиология
- Специальности Биология / Биология высшего уровня
- Микробиология
- Неосновная биология
- Химия
- Наука об окружающей среде
- География и атмосферные науки
- Геология и океанография
- Здоровье и кинезиология
- Математика
- Продвинутая математика
- Исчисление
- Развивающая математика
- Конечная математика и прикладное исчисление
- Гуманитарные науки Математика / Математика для учителей
- Математика для карьеры
- Математика
- Математика Precalculus
- Техническая математика
- Питание
- Физика и астрономия
- Статистика
- Вводная статистика
- Статистика верхнего уровня
- Профессиональная карьера
- Бизнес
- Бухгалтерский учет и налогообложение
- Деловые коммуникации
- Предпринимательское право
- Бизнес-математика
- Деловые навыки
- Наука принятия решений
- Финансы
- Страхование
- Введение в бизнес
- MIS
- Управление
- Маркетинг
- Офисные Технологии
- Деловая статистика
- Коммуникационные науки и расстройства
- Информационные технологии
- Консультации
- Уголовное правосудие
- Кулинария, гостиничный бизнес, путешествия и туризм
- Кулинарное искусство
- Наука о еде
- Гостеприимство
- Путешествия и туризм
- Исследования глухих и образование глухих
- Экономика
- Образование
- Учебный план и инструкция
- ELL
- Дошкольное образование
- Ed Psych / Тесты и измерения
- Управление образованием и лидерство
- Образовательные исследования
- Основы / Введение в обучение
- Учебные технологии
- Подготовка лицензии
- Чтение и грамотность
- Специальное образование
- EMS и пожарная наука (BRADY)
- Скорая медицинская помощь (BRADY)
- Наука о пожаре (BRADY)
- Инженерное дело
- Биоинженерия
- Химическая инженерия
- Гражданская и экологическая инженерия
- Электротехника и вычислительная техника
- Общая инженерия
- Промышленная инженерия
- Машиностроение и аэрокосмическая техника
- Техническая математика / Техническая физика
- Мода и дизайн интерьера
- Потребительская наука
- Мода
- Дизайн интерьера
- Медицинские профессии
- Базовые курсы здоровья
- Клиническая лабораторная наука
- Стоматологическая помощь
- Гигиена полости рта
- Управление медицинской информацией
- Массажная терапия
- Медицинская помощь
- Кодирование медицинского страхования
- Медицинская терминология
- Медицинская транскрипция
- Младшая медсестра
- Трудотерапия
- Аптечный служащий
- Флеботомия
- Физиотерапия
- Хирургическая техника
- Дыхательная терапия
- Информационные технологии
- СНГ: вычислительные концепции
- СНГ: офисные приложения
- Компьютерная графика / Искусство
- Разработка игр
- Безопасность
- Обучение и сертификация
- Юридические исследования и помощник юриста
- Уход
- LPN / LVN
- RN
- Успех студентов и развитие карьеры
- Торговля и технологии
- сельское хозяйство
- Автомобильная техника
- Строительные и технические работы
- САПР / Инженерная графика / Черчение
- Управление строительством и гражданские технологии
- Электроника и электроэнергетика
- Инженерные технологии и промышленный менеджмент
- Экологические технологии
- Технические сделки: NCCER / Contren
- Бизнес
- Изучающие английский язык
- Войдите, чтобы загрузить ресурсы инструктора
- Скачивание и использование инструкторских ресурсов
- Гуманитарные и социальные науки
- Продукты и услуги для обучения
- Цифровая среда обучения
- Веселье
- MyLab
- Освоение
- Учебная программа по концепциям медсестер
- Льготы
- Начать
- Отзывы
- Обучение и поддержка
- Редакторы и авторы
- Район 3.0
- Содержание курса
- Учебники и электронные тексты
- Электронный текст Пирсона
- Системные Требования
- Мобильное приложение Pearson eText
- Электронный текст Пирсона
- Коллекции Пирсона
- Учебники и электронные тексты
- Решения для дистанционного обучения
- Системы обучения действиям
- CourseConnect
- Поддержка
- Педагоги, начните
- Студенты, начните
- FAQs
- Системные Требования
- Поддержка
- NCCERconnect
- Характеристики
- Доступные названия
- Поддержка
- Поддержка преподавателей
- Студенческая поддержка
- Системные Требования
- Pearson Workforce Education
- Проперо
- Для студентов
- Как работает Проперо
- Опыт курса
- Получение кредита колледжа
- Homeschool / Учащиеся до 12 лет
- Военнослужащие
- Работающие профессионалы
- Для преподавателей и учебных заведений
- Как работает Проперо
- Академическое качество
- Академические руководители
- Факультет
- Студенто-ориентированное обучение
- Корпоративное обучение
- Партнеры
- Курсы
- Истории успеха
- Отзывы студентов
- Отзывы преподавателей
- Поддержка
- Системные Требования
- Техническая поддержка
- Запросить дополнительную информацию
- Для студентов
- Виртуальная академия EMS
- Инструменты обучения и взаимодействия
- Приложение для обучения Aida Calculus
- Обучение каталитике
- Характеристики
- Истории пользователей
- Развитие навыков критического мышления
- Цифровая среда обучения
Преподавание математики с помощью концептуальной мотивации и обучения действиям
Это концептуальный документ, основанный на практических примерах, описывающий избранные средства обучения действиям и концептуальную мотивацию на всех уровнях математического образования.В нем подробно описывается подход, использованный авторами для разработки идей для практиков преподавания математики. В статье показано, что такой подход в математическом образовании, основанный на практическом обучении в сочетании с естественной мотивацией, проистекающей из здравого смысла, является эффективным. Кроме того, стимулирующие вопросы, компьютерный анализ (включая поиск в Интернете) и классические известные задачи являются важными инструментами мотивации в математике, которые особенно полезны в рамках практического обучения. Авторы утверждают, что вся учебная программа по математике K-20 под единым зонтом возможна, когда методы концептуальной мотивации и обучения действиям используются во всем этом широком спектре.Этот аргумент подтверждается различными примерами, которые могут быть полезны на практике школьным учителям и преподавателям вузов. Авторы нашли прагматическую причину для практического обучения математике практически на любом этапе академической жизни студентов.
1. Введение
В настоящее время студентам требуется как познавательный, так и практический опыт на протяжении всего их математического образования, чтобы быть продуктивными гражданами 21 века. Происхождение этого утверждения можно проследить до работ Джона Дьюи, который подчеркивал важность образовательной деятельности, которая включает «развитие любого рода артистических способностей, особых научных способностей, эффективных гражданственности, а также профессиональных и деловых качеств». профессий »([1], с.307). Совсем недавно Биллетт [2], основываясь на своих исследованиях интеграции опыта обучения студентов высших учебных заведений в дисциплинах, связанных с сестринским уходом и подобными услугами в поддержку человеческих потребностей, предположил, что «возможно, можно будет полностью интегрировать практический опыт в совокупность опыта высшего образования, которая способствует развитию прочных и критических профессиональных знаний »(стр. 840). Главный аргумент настоящей статьи состоит в том, что в контексте математического образования практическое обучение (концепция, представленная в разделе 3) — это сам процесс передачи этого опыта в сочетании с концептуальной мотивацией (термин, введенный в разделе 2) при обучении математике. по всей учебной программе K-20.С этой целью в этом практическом концептуальном документе, подробно описывающем подход, использованный авторами для разработки идей для практиков преподавания математики, предлагается обзор избранных средств практического обучения в рамках формального континуума математического образования. В определенной степени эта статья продвигает идею обучения на практике [3] в контексте математического образования. Представлены аргументы, подтверждающие ценность практического обучения для всех вовлеченных лиц (на уровне колледжа, добавление к дуэту студента и преподавателя математики третьего сообщества или университетского профессионала-нематематика) (разделы 2–4).Также рассматривается интеграция компьютерной педагогики сигнатур (CASP) и нецифровой технологии, а также эффективное опросы с обучением действием (разделы 5 и 6).
Студенты могут с радостью получать формальное математическое образование в течение двадцати и более лет, и они могут быть мотивированы повсюду с помощью обширных учебных программ по математике. Практическое обучение в математическом образовании в сочетании с механической теорией переносит математические темы в реальный мир. Естественно, что примеры начального уровня имеют основополагающее значение, и это подкрепляется практическим обучением на вторичном уровне (разделы 4.1.1 и 4.1.2). Открытые проблемы математики часто могут быть представлены учащимся начальных, средних и высших учебных заведений (Раздел 7). Традиционно классические результаты и открытые задачи мотивируют не только студентов, но и самих педагогов. Поскольку необходимы эффективные учителя математики, практическое обучение следует использовать на всех уровнях математического образования, зная, что будущие преподаватели входят в число нынешних учащихся. Конечно, возможность участвовать в открытиях очень мотивирует всех, включая студентов и учителей математики, по крайней мере.
2. Любопытство и мотивация
Хотя необходимость изучения математики в начальной, средней и высшей школе общеизвестна, вопрос о том, как преподавать математику, остается спорным. Как более подробно описано в [4] со ссылками на [5–10], разногласия связаны с неоднородностью программ подготовки учителей, разногласиями между формализмом и смыслом между преподавателями математики и различными взглядами на использование технологий. Мы считаем, что надлежащий способ преподавания математики на всех уровнях — это делать это через приложения, а не использовать традиционные лекции, подчеркивая формализм математического аппарата.Реальные приложения позволяют заинтересованным людям учиться математике. Эту естественную мотивацию можно рассматривать как зависящий от возраста процесс, простирающийся от естественного детского любопытства в начальной школе до истинного интеллектуального любопытства на уровне высшего образования. Независимо от возраста учащихся, можно рассматривать любопытство как мотивацию «приобретать или преобразовывать информацию в обстоятельствах, которые не представляют немедленной адаптивной ценности для такой деятельности» ([11], с. 76). То есть любопытство и мотивация — тесно связанные психологические черты.
Большинство исследований, посвященных развитию любознательности, касается начального образования. Однако эти исследования могут помочь нам понять, как любопытство превращается в мотивацию стать высококлассным профессионалом. Например, Видлер [12] проводил различие между эпистемическим и перцептивным любопытством, которые проявляются, соответственно, «запросом о знании» и проявляются, например, когда ребенок ломает голову над какой-то научной проблемой, с которой он столкнулся… [и] повышенное внимание данные объектам в ближайшем окружении ребенка, например, когда ребенок дольше смотрит на асимметричную, а не симметричную фигуру на экране »(стр.18). Точно так же взрослые учащиеся на высшем уровне могут быть мотивированы призывом своего учителя математики задать вопросы, касающимся информации, которой они поделились, или их опытом общения с окружающим миром, когда они пытаются интерпретировать «ткань мира… [используя] некоторые причины максимум и минимум »(Эйлер, цит. по [13], с. 121).
Связанный с высшим уровнем, Видлер [14] определил мотивацию достижения как «образец… действий… связанных со стремлением достичь некоего усвоенного стандарта качества» (стр.67). Есть также взрослые ученики, которые «заинтересованы в совершенстве ради него самого, а не ради вознаграждения, которое оно приносит» ([14], с. 69). Биггс [15] признает, что внутренняя мотивация в изучении математики связана с «интеллектуальным удовольствием от решения проблем независимо от каких-либо вознаграждений, которые могут быть вовлечены… [предполагая, что] цели глубокого обучения и мотивации достижения в конечном итоге расходятся» (стр. 62). Классическим примером в поддержку этого предположения является решение гипотезы Пуанкаре (столетней давности), выполненное геометром Григорием Перельманом, который после почти десятилетия «глубокого обучения» отказался от нескольких международных наград за свою работу, включая медаль Филдса («Медаль Филдса»). Нобелевская премия ») и (1 миллион долларов) Clay Millennium Prize (https: // www.Claymath.org/).
Поскольку любопытство является источником мотивации к обучению, Мандельброт [16] в пленарной лекции по экспериментальной геометрии и фракталам на 7-м Международном конгрессе по математическому образованию посоветовал аудитории, состоящей в основном из преподавателей математики дошкольного образования, как сосредоточиться на любопытстве, когда преподавание математики: «Мотивируйте учащихся тем, что увлекательно, и надейтесь, что возникающий энтузиазм создаст достаточный импульс, чтобы продвинуть их через то, что не весело, но необходимо» (стр.86). Именно такую мотивацию авторы называют концептуальной мотивацией. В частности, в этой статье термин «мотивация концепции» означает стратегию обучения, с помощью которой, используя любопытство учащихся в качестве стержня, введение новой концепции оправдывается за счет ее использования в качестве инструмента в приложениях для решения реальных проблем. Например, операция сложения может быть мотивирована необходимостью записать увеличение большого количества
.






 Куда поставить кубик с 7 точками?).
Куда поставить кубик с 7 точками?). п.).
п.). Вслух рассказывайте о том, что вы делаете. Показывайте собственную заинтересованность процессом игры. Ребенок увидит ваш интерес и присоединится;
Вслух рассказывайте о том, что вы делаете. Показывайте собственную заинтересованность процессом игры. Ребенок увидит ваш интерес и присоединится;
 Б. (21)
Б. (21) Андерсен (47)
Андерсен (47) (2)
(2)

 Эта способность развивается постепенно. Вначале вы должны помочь своему ребенку.
Эта способность развивается постепенно. Вначале вы должны помочь своему ребенку.