Развивающая математика: Книга: «Развивающая математика. 1-4 классы. Формирование познавательно-математической деятельн. ФГОС (+СD)» — Наталья Лободина. Купить книгу, читать рецензии | ISBN 9785705750146
РАЗВИВАЮЩАЯ МАТЕМАТИКА
Ведущие:
Втюрина Елена Станиславна
Знать и понимать математику важно не только тем, кто собирается работать в области науки и техники. Как говорил М.В. Ломоносов, «Математику уже затем учить надо, что она ум в порядок приводит».
Программа, разработанная для дошкольников и младших школьников, направлена на то, чтобы:
- создать у детей позитивный эмоциональный настрой на занятия математикой, показать, что математика — это интересно, красиво и весело;
- дать учащимся все необходимые математические знания, представления и навыки, необходимые для учебы в школе;
- найти и развить в детях математические способности и подготовить к участию в математических олимпиадах;
- способствовать развитию у детей логического, абстрактного и творческого мышления, памяти, внимания, воображения, произвольности, умения общаться;
Данная программа разработана на основе системы учебно-методических материалов, созданных ведущими специалистами в области обучения детей математике: программы Е.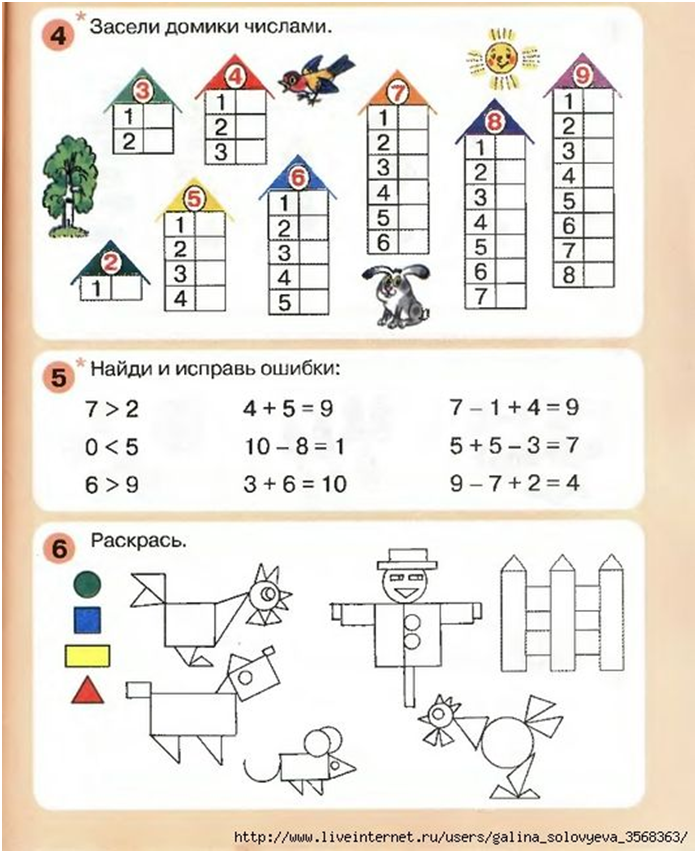
Расписание занятий
Ф.И.О. преподавателя
Группы/Индивидуальные занятия
Место проведения
Дни занятий
Время проведения занятий
Втюрина
Елена Станиславна
Гр.
 1 (4-ые классы)
1 (4-ые классы)«Гримау 6»
вторник
16.00 — 16.50
16.00 — 16.50
Гр.2 (3-е классы)
«Гримау 6»
вторник
четверг
17.00 — 17.50
17.00 — 17.50
9 лучших настольных развивающих игр по математике
Фаталисты считают, что судьба человека определена с рождения, но психологи заверяют: будущее ребёнка — в руках родителей! От того, какие игры выберете вы для своего чада, зависит развитие его мозга, раскрытие способностей, преумножение талантов. Если второклассник швыряет в стену учебник математики, а старшеклассник спрашивает, на кой чёрт ему эти синусы и косинусы, — можно со 100 %-ной уверенностью сказать, что у бедняги никогда не было увлекательных математических игр.
Набор математических настольных игр — это ракета-носитель, которая выведет ребёнка на орбиту жизненного успеха. И дело не только в хороших оценках, выигранных олимпиадах и высоких баллах ЕГЭ (это само собой!).
- Математическое мышление — это логический, структурированный, системный, аналитический подход к решению задач во всех сферах жизни.
- Математику не зря называют царицей наук, ведь без неё невозможны научные исследования, открытия и инновации.
- Математика полезна не только будущим «технарям» и «физикам», но и «лирикам». Архитектура, музыка, скульптура, даже живопись и поэзия строятся на незыблемых математических законах гармонии.
- Математика — это тренажёр для мозга. Совершая в математических настольных играх маленькие открытия, ребёнок становится любопытней, раскрывает для себя красоту и глубину законов Вселенной, развивает логику, улучшает когнитивные функции мозга, становится настоящим исследователем!
Заманчиво? Конечно, ведь каждый родитель хочет для своего ребёнка лучшего! И главное, любовь к математике прививается ненавязчиво, в игровой форме. Это не «училка» заставляет мучиться с домашними заданиями, это сам ребёнок становится Пифагором, Лейбницем и Декартом!
Это не «училка» заставляет мучиться с домашними заданиями, это сам ребёнок становится Пифагором, Лейбницем и Декартом!
Но некоторые родители идут простым путём: дают в руки малышу планшет со скачанными математическими играми. И совершают огромную ошибку, ведь компьютерные программы, даже самые увлекательные, не сравнятся по эффективности с настольными логическими играми по математике.
Компьютер VS настольной игры
Вряд ли кто-то из психологов одобрит вручение малышу ясельного возраста гаджета с компьютерными играми. А вот обучать кроху счёту в игровой форме — это полезно! У ребёнка до 3-х лет мозг поразительно гибок, и это время никак нельзя упустить. Взросления, дошкольники начинают в игровой форме осваивать арифметические действия, а школьники — постигать чрез игру более сложные законы математики. И будет лучше, если развивающие игры окажутся настольными.
- Даже самые полезные обучающие программы грозят компьютерной зависимостью, особенно если у ребёнка нет альтернативы.

- Усаживая детей за планшет или ноутбук, вы заставляете их общаться с искусственным интеллектом. А в настольные игры по математике ребёнок играет с вами. За некоторые можно засесть всей семьёй! Укрепляются семейные связи, развиваются коммуникативные навыки.
- Занимательные настольные игры ненавязчиво развивают мелкую моторику, способствуют улучшению концентрации и внимания.
- И зрение, что немаловажно, не страдает!
Какие же математические игры для девочек и мальчиков выбрать, учитывая возраст? С чего начать, обучая счёту малыша, и какие продвинутые математические забавы подойдут для школьника?
Перед вами — список топовых игр, получивших самые высокие оценки и массу положительных отзывов от родителей, психологов, педагогов и самих детей.
7 на 9 — раскрути мозги на полную катушку!
Возраст: от 8 лет
Число игроков: 2 — 4
Это карточная математическая игра, созданная для детей младшего школьного возраста, но в неё можно играть даже с дошкольниками, поскольку правила строятся вокруг сложения и вычитания в пределах десятки. На каждой карте — две цифры: большая и маленькая. Например, 5 и 2. Значит, побить эту карту можно той, на которой число является результатом сложения (5 + 2) или вычитания (5 — 2).
На каждой карте — две цифры: большая и маленькая. Например, 5 и 2. Значит, побить эту карту можно той, на которой число является результатом сложения (5 + 2) или вычитания (5 — 2).
Но и взрослые, начав играть в «7 и 9», оторвутся с трудом — настолько игра азартна! Для драйва можно включить таймер и считать на скорость. А школьники постарше с помощью «7 и 9» смогут научиться легко оперировать отрицательными числами.
Цветариум — создай империю цветов!
Возраст: от 7 лет
Число игроков: 2 — 5
Это математическая игра, которая больше всего понравится девочкам, ведь тут нужно разбивать клумбы, бороться с вредителями, выращивать цветочки и продавать всю эту красоту. Особенность настольной цветочной «фермы» — в правилах, которые базируются на принципах умножения.
В общем, идеальный способ выучить таблицу умножения без слёз. Яркая и динамичная математическая игра для продвинутых дошкольников и учеников 1 — 2 класса.
Много-много — умножай и строй!
Возраст: от 5 лет
Число игроков: 2 — 5
Интересная и обучающая игра — 2 в 1. Облегчённый вариант развивает навыки счёта у малышей, которые ищут в окошках домиков цифры, выпавшие на картах. Более сложный вариант обучает умножению и развивает стратегическое мышление. Игроку нужно построить много-много домиков, выполняя задания на умножение, и азартно соревнуясь с конкурентами!
Облегчённый вариант развивает навыки счёта у малышей, которые ищут в окошках домиков цифры, выпавшие на картах. Более сложный вариант обучает умножению и развивает стратегическое мышление. Игроку нужно построить много-много домиков, выполняя задания на умножение, и азартно соревнуясь с конкурентами!
Геометрика — становись Евклидом!
Возраст: от 7 лет
Число игроков: 2 — 8
Эта занимательная игра отправляет юного геометра в мир треугольников, многоугольников, прямых и кривых. Играть можно даже с дошкольником, постепенно наращивая сложность. Да и родителям будет полезно вспомнить, есть ли у линии периметр или как называется треугольник без единого прямого угла. Со скучными учебниками не сравнить. Каждый день, совершая новые открытия, ребёнок влюбится в геометрию!
Сундучок знаний: Мир математики — кто тут главный эрудит?
Возраст: от 7 лет
Число игроков: 1 — 10
В этом ярком сундучке — целый клад для юного математика, готовящегося к школе или уже грызущего гранит науки.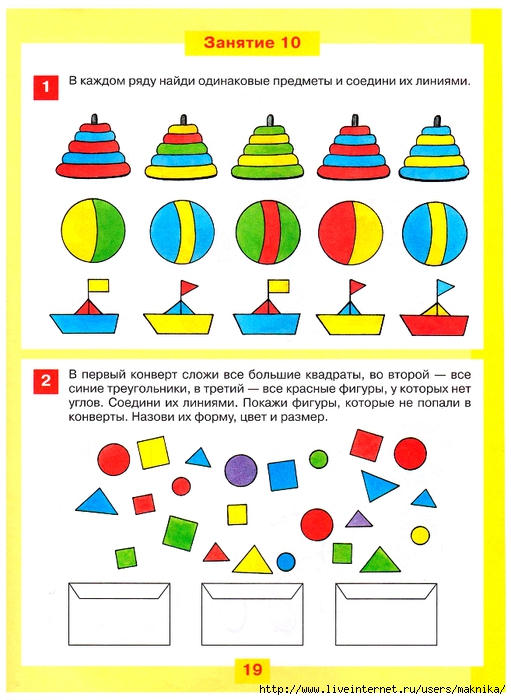 Математическая игра в формате викторины — увлекательный и азартный способ познакомиться с кубами и пирамидами, конусами и сечениями, принципами симметрии и другими умными штуками. На одной стороне карты — информация, которую нужно запомнить, пока сыплются песчинки в настольных часах. На другой — вопросы. А ну, не подглядывать назад!
Математическая игра в формате викторины — увлекательный и азартный способ познакомиться с кубами и пирамидами, конусами и сечениями, принципами симметрии и другими умными штуками. На одной стороне карты — информация, которую нужно запомнить, пока сыплются песчинки в настольных часах. На другой — вопросы. А ну, не подглядывать назад!
Тренироваться можно в одиночку, соревноваться — всей семьёй или весёлой компанией.
Делиссимо — мне четвертинку пиццы, и не задерживайте!
Возраст: от 6 лет
Число игроков: 2 — 5
Натуральные дроби — бич среднестатистического школьника. Но если вы подарите ребёнку игру «Делиссимо», дроби перестанут быть проблемой. В лёгком варианте игры он на примере деления пиццы наглядно увидит, что представляют собой эти ужасные дроби — и без труда с ними подружится. А в более сложном — научится выполнять замороченные заказы клиентов пиццерии, которые в одном заказе требуют, представьте себе, половинку пиццы с морепродуктами и 1/8 с томатами!
А вы сами-то не растеряетесь, выполняя такой заказ?
Математика: Сложение и вычитание — ярко и понятно!
Возраст: от 5 лет
Число игроков: от 1
Перед вами — обучающая игра в математику для малышей, приступающих к постижению загадочного мира чисел. Яркие картинки и красивые магнитики увлекут ребёнка и помогут ему запомнить цифры, а затем — научиться складывать и вычитать. В комплекте — куча карточек, магнитов, маркер и рабочая тетрадка. Можно поиграть в школу и убедить малыша, что на уроках математики будет интересно!
Яркие картинки и красивые магнитики увлекут ребёнка и помогут ему запомнить цифры, а затем — научиться складывать и вычитать. В комплекте — куча карточек, магнитов, маркер и рабочая тетрадка. Можно поиграть в школу и убедить малыша, что на уроках математики будет интересно!
Руммикуб — для азартной компании
Возраст: от 7 лет
Число игроков: от 2 — 4
Если вы считаете, что игры с математическим содержанием — это для малышей, ну в крайнем случае для младших школьников, то «Руммикуб» развеет ваши стереотипы. Это игра, изобретённая 70 лет назад в Румынии, рассчитана на всех: и на детей, и на подростков, и на взрослых. На просторном игровом поле найдётся место для четырёх карточных мастей, вот только вместо карт — деревянные фишки с цифрами. В самых продвинутых вариантах «Руммикуб» сложнее шахматных баталий, в облегчённых — подходит для детворы.
Озадачник математика — ну-ка, озадачимся!
Возраст: от 6 лет
Число игроков: от 1
Весёлые и мудрёные задачки — лучший способ заставить извилины шевелиться. Эта математическая игра для детей не раз поставит в тупик и взрослого, потому что здесь мало использовать арифметические правила — нужно включать смекалку. Кроме того, хорошее настроение гарантировано: задачки-озадачки составляли юмористы!
Эта математическая игра для детей не раз поставит в тупик и взрослого, потому что здесь мало использовать арифметические правила — нужно включать смекалку. Кроме того, хорошее настроение гарантировано: задачки-озадачки составляли юмористы!
Все игры с математическим уклоном собраны в категории «Математические настольные игры». Выбирайте!
Хотите уточнить правила заинтересовавшей игры или посоветоваться, какую выбрать для своего ребёнка? Звоните по бесплатному номеру
Математика для детей 7-8 лет
В обучении ребенка родители играют не меньшую роль, чем школьные преподаватели. Разумеется, примеры и задачки по математике для детей 7 лет кажутся взрослым совсем простыми. Но понимать задание и делиться собственными знаниями — вовсе не одно и то же. Онлайн-упражнения по математике для ребенка 7 лет, представленные в соответствующем разделе, призваны помочь в развитии маленького ученика и улучшить усвоение им нового материала. Обучение на сайте «Разумейкин» позволит заинтересовать ребенка миром цифр и облегчить процесс его адаптации к школе.
Обучение на сайте «Разумейкин» позволит заинтересовать ребенка миром цифр и облегчить процесс его адаптации к школе.
Задания по математике для детей 7 лет знакомят ребят с числами второго десятка. Справляясь с ними, малыши учатся считать без перехода через десяток и с переходом через десяток. Кроме того, ребята осваивают счет в пределах ста. Развивающие задания в разделе «Математика для детей 8 лет» будут интересны и полезны ученикам 1-2 классов. Выполняя их, ребята смогут отработать и закрепить пройденный материал.
Задания-тесты по математике для детей 7 лет позволяют осваивать эту точную науку в форме обучающей игры. Разрабатывая упражнения, специалисты сайта «Разумейкин» стремились сделать их не только максимально понятными и увлекательными, но и действительно полезными в практическом плане. Для каждой задачи для детей 7 лет по математике представлено подробное объяснение. Найти его можно в обучающем видео перед упражнением. Соответствующее объяснение к заданиям по математике для дошкольников, школьников 7 лет и старше предоставляется также в ситуации, когда ребенок дал неправильный или недостаточно полный ответ.
Как подается обучающий материал?
Чтобы развивающие игры в разделе «Математика для детей 7 лет» давались юным непоседам легко и были действительно интересными, сотрудники сайта «Разумейкин» дополнили каждое упражнение тематическими картинками. Кроме того, в них присутствует аудиососпровождение, а некоторые задачи даже задействуют двигательную сферу. Все задания-игры в разделе «Математика для детей 7-8 лет» можно выполнить в онлайн-режиме.
Как осуществляется оценка результатов?
Специалисты развивающего сайта «Разумейкин» разработали целую систему поощрений. Справляясь с заданиями по математике, дошкольники, школьники 7 лет и более старшие дети получают виртуальные награды. На нашем сайте предусмотрены медали, кубки, вымпелы и грамоты. Мы убеждены, что таким образом можно повысить интерес ребят к самостоятельному обучению и выработать положительную мотивацию.
Практически все задачи-игры в разделе «Математика для детей 8 лет» оцениваются в зависимости от того, с какой попытки ребенок дал правильный ответ.
Ваш ребенок уже готов начать обучение? Предварительно мы рекомендуем пройти тестирование. Полученные результаты помогут понять, на каких темах потребуется остановиться более детально. Кроме того, родители смогут определить, какие именно упражнения в разделе «Математика для детей 8 лет» лучше выполнить в первую очередь.
App Store: Фиксики. Математика для детей
Лучшая развивающая игра для детей. Математика для детей. Арифметика. Учим цифры, формы, часы вместе с героями мультфильма Фиксики!
Задания продуманы детскими психологами для легкого обучения ребенка арифметике. Лучшая обучающая игра по мнению родителей.
Лучшая обучающая игра по мнению родителей.
Большая часть опрошенных детей, благодаря игре, уже через неделю смогла верно отвечать на
простые вопросы по математике и называть время по часам.
Обучение математике детей при подготовке к школе уже протестировано в старших группах детских садов и признано педагогами как полезное. Воспитатели оказались очень довольны результатами и включили детские игры в общий план занятий групп.
ОБРАЗОВАТЕЛЬНОЕ СОДЕРЖАНИЕ
В играх для детей Фиксики помогут разобраться в следующих вопросах:
— Учим счет и количество
– Состав числа
– Сложение и вычитание от 1 до 20
– Считаем десятками
– Знакомимся с монетами
— Рассматриваем формы фигур
– На какую форму похож предмет?
– Что такое многоугольники?
– Логический квадрат
— Ориентируемся в пространстве
– Рисуем по клеточкам
– Лево-право
– Заряжаем батарейку (налево-направо-вверх-вниз)
— Знакомимся с часами, со счетом времени. Крутим стрелки и выставляем время на часах.
Учить счет для ребенка будет не скучно, для этого мы придумали приключение. Герои мультфильма Фиксики строят ракету из частей, решая задания по математике. Построим ракету вместе!
Обучающее математике приложение разработано специально для детей в возрасте от 5 лет и
старше, насыщено анимациями и красочной графикой, полностью озвучены персонажи
и задания, интерфейс прост и понятен ребёнку.
Ваш ребенок 5–7 лет полюбит развивающие игры с Фиксиками. Фиксики учат математике – родители отдыхают!
Игра содержит интересные развивающие уровни. Детские игры бесплатно. В бесплатной версии приложения доступна часть контента. Чтобы получить полную версию, вам необходимо совершить встроенную покупку.
Мы продолжаем разработку приложения для детей, и все новые уровни вы получите бесплатно, просто обновив его в магазине.
Если Вам понравилась математика с героями мультика Фиксики – поставьте, пожалуйста, оценку нашей развивающей игре для детей, чтобы рекомендовать нас другим пользователям.
1C-Publishing LLC
Если вам нравится то, что мы делаем, и есть желание присоединиться к нам, вы сможете сделать это здесь:
Сайт разработчика:
http://obr.1c.ru/educational/uchenikam/matematika-dlya-detey-fiksiki/?utm_source=play_market&utm_medium=cpc&utm_campaign=fixik_math_descrip
Канал youtube:
https://www.youtube.com/channel/UClopWz9n4jhkQqCfOMfMnBA?utm_source=play_market&utm_medium=cpc&utm_campaign=fixik_math_descrip
Группы «ВКонтакте»:
https://vk.com/educational_programs?utm_source=play_market&utm_medium=cpc&utm_campaign=fixik_math_descrip
Группы «Одноклассники»:
https://www.ok.ru/obrazov?utm_source=play_market&utm_medium=cpc&utm_campaign=fixik_math_descrip
Группы «Facebook»:
https://www.facebook.com/1C.Obr/?utm_source=play_market&utm_medium=cpc&utm_campaign=fixik_math_descrip
УМНИК. Математика: интерактивные развивающие задания, 5 класс
Интерактивные развивающие задания могут служить полезным дополнением к любым учебникам математики для 5 классов. Задания носят мотивирующий характер и предназначены для стимулирования интереса учащихся к содержанию изучаемого курса.
Задания носят мотивирующий характер и предназначены для стимулирования интереса учащихся к содержанию изучаемого курса.
Демонстрационная версия
Книжка для детей и родителей
Скачать установочный файл MathGames5Lic.air (Windows/Mac)
Издательство «Лаборатория базовых знаний»,
Компьютерная реализация – «Мультимедиа-студия «Март»
Интерактивное приложение состоит из восьми блоков, каждый из которых посвящен одной из тем, изучаемых в курсе математики 5 класса: «Счет, цифры, позиционные системы счисления», «Меры», «Обыкновенные дроби», «Действия с натуральными числами: сложение и вычитание», «Умножение натуральных чисел и десятичных дробей», «Деление», «Отрицательные числа, сложение и вычитание», «Умножение и деление чисел со знаком».
Каждая тема раскрывается на примере ситуационной модели и представляется учащемуся в четырех различных форматах, имеющих разное назначение и отличающихся по степени интерактивности.
«Мультимедийный клип». Первая часть блока, которая представляет собой анимационный сюжет, задающий тему блока. Клип представляет описание игровой ситуации, в которой герои сталкиваются с некоторой проблемой, решение которой связано с определенными математическими действиями. Длительность каждого клипа составляет порядка 1 мин, визуальный ряд сопровождается стихотворным текстом. Предлагаемый сюжет ставит проблему, но не отвечает на вопрос.
Первая часть блока, которая представляет собой анимационный сюжет, задающий тему блока. Клип представляет описание игровой ситуации, в которой герои сталкиваются с некоторой проблемой, решение которой связано с определенными математическими действиями. Длительность каждого клипа составляет порядка 1 мин, визуальный ряд сопровождается стихотворным текстом. Предлагаемый сюжет ставит проблему, но не отвечает на вопрос.
«Диафильм». Для более детального просмотра описанной проблемной ситуации содержание мультипликационного клипа дополнительно представляется в виде набора статичных кадров с подписями. Это позволяет учащемуся останавливаться на каждом ключевом кадре, анализировать ход сюжета и реплики героев, то есть получить полное представление о ситуационной модели и проблеме, которая требует решения.
«Схема». Третья часть нацелена на осуществление постепенного перехода от игровой ситуации к математической проблеме. Она реализуется так же в в виде набора слайдов, визуальное решение которых основано на художественных образах, знакомых учащемуся по предыдущим частям. При этом в нижней части слайдов добавлены схематичные иллюстрации, которые предоставляют возможность учащемуся проследить, как решение проблемы, поставленной в рамках игровой ситуации, реализуется математическими методами. Такой подход призван облегчить учащимся формализацию решаемой проблемы, поддержать переход от конкретной ситуации к ее математической трактовке и как следствие способствуют переходу от ситуационной модели к математической.
При этом в нижней части слайдов добавлены схематичные иллюстрации, которые предоставляют возможность учащемуся проследить, как решение проблемы, поставленной в рамках игровой ситуации, реализуется математическими методами. Такой подход призван облегчить учащимся формализацию решаемой проблемы, поддержать переход от конкретной ситуации к ее математической трактовке и как следствие способствуют переходу от ситуационной модели к математической.
«Мини-лаборатория». Понимание учащимся математической сущности поставленной проблемы закрепляется в формате интерактивных тренингов. Данное приложение предоставляет возможность поработать с математической моделью, обобщить рассмотренную в сюжете ситуацию, уяснить себе закономерности, лежащие в основе тех или иных математических операций. В каждой мини-лаборатории учащимся предлагается несколько заданий (от 2 до 3), которые выстроены от простого к сложному. Конкретные числовые значения генерируются случайным образом, что позволяет учащимся практиковаться в решении типовых задач.
Все части объединены общей стилистикой. В них действуют одни и те же персонажи, что обеспечивает учащимся возможность осваивать весь курс, оставаясь в рамках одной и той же игровой модели.
Демонстрационная версия даст вам представление о содержании всех частей программы.
Скачать установочный файл MathGames5Lic.air
Книжка для детей и родителей: скачать бесплатно pdf-файл
Внимание! Установочный файл MathGames5Lic.air — кросс-платформенная (Windows/MacOS X) версия программы на Adobe AIR. Запустить кросс-платформенную версию Вы сможете только если для Вашей операционной системы доступна среда Adobe AIR
Чтобы приобрести лицензию на программу:
— зарегистрируйтесь на сайте или войдите под своим именем;
— добавьте в заказ лицензию;
— перейдите в раздел оформления заказа и оплатите его;
— получите лицензионный ключ на указанный Вами адрес электронной почты.
Чтобы начать работу с кросс-платформенной (Windows/MacOS X) версией программы на Adobe AIR:
— загрузите и установите Adobe Air для Вашей операционной системы
— сделайте два клика на файл установки приложения для air (MathGames5Lic. air)
air)
— следуйте инструкциям по установке air-приложения
— при первом запуске приложения введите данные полученного лицензионного ключа
Важно! При установке программы на компьютер необходим активный доступ в Интернет.
Программа имеет версии для мобильных платформ:
| Android: | iPad, iPhone: |
|---|---|
| | |
| Файл для скачивания | Размер |
|---|---|
| MathGames5Lic.air — кросс-платформенная версия (Windows/MacOS X) на Adobe AIR | 18.15 Мбайт |
| Книжка для детей и родителей (pdf) | 2.38 Мбайт |
Дополнительная программа «Развивающая математика – старт»
1 год обучения — 72 часа
1. Виды счёта – 10 часов
Счёт предметов: прямой, обратный, порядковый, количественный. Числа – соседи. Чётные и нечётные числа. Образование «семеек». Счёт парами.
Образование «семеек». Счёт парами.
2. Сравнение предметов и совокупностей – 20 часов
Теория
Свойства предметов (цвет, форма, размер, толщина).
Объединение предметов в группы по сходным признакам (двум, трём).
Сравнение предметов по цвету, форме, толщине, размеру.
Измерение с помощью условной мерки.
Практика
Дидактические игры: «Найди свой дом», «Муравьишки по домам», «Найди клад», «Поезд», «Где чей дом», «Автотрасса», «Выращивание дерева», «Два обруча» и другие.
3. Образование и состав числа – 17 часов
Теория
Состав числа от 2 до 10. Домики. Составление и решение задач по карточкам, используя палочки Кюизенера. Сложение и вычитание. Решение примеров.
Практика
Дидактические игры: «Коврик», «Вычислительные машины», «Логические цепочки», » Число и цвет«, «Весёлый поезд», «Сломанная лесенка» и другие.
4. Пространственно-временные представления – 13 часов
Теория
Ориентация на листе бумаги, в пространстве, во времени.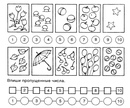
Понятия «вправо-влево», «впереди-сзади», «внизу- вверху», «близко-далеко», «маленький-большой», «раньше-позже», «вчера-сегодня», дни недели, месяцы, времена года. и т.д.
Практика
Дидактические игры: «Покорми белочку», «Логический поезд», «Далеко-близко», «Угадай день» и другие.
5. Поиск закономерностей — 11 часов
Теория
Последовательность событий, цепочка событий, закономерности расположения предметов, деление блоков по признакам и распределение по «домикам»,.Доказательства поисковых ситуаций во время игры..
Практика
Дидактические игры: «Автотрасса», «Цепочка», «Больше, меньше, столько же», «Давайте познакомимся», «Найди клад», «Помоги друзьям».
Игры – головоломки: «Танграмм», «Пифагор», «Колумбово яйцо», «Монгольская игра» и другие.
5. Заключительное занятие — 1 час
Игра: «Поиграем в математику»
Развивающая игра «МногогранникУм»
Презентация развивающей математической игры «МногогранникУм».
Бывает, что во время урока математики, когда даже воздух стынет от скуки,
в класс со двора влетает бабочка …
А.П. Чехов
Актуальность игры «МногогранникУм». «У меня не получается. У меня нет способностей к математике. Я гуманитарий», — эти оправдания каждый учитель математики слышал неоднократно. Как и слова родителей о нежелании учиться и переходном возрасте. Но, если проанализировать эти ситуации, обнаруживаем следующее. Ученику не хватает элементарных математических и метапредметных навыков. Математика – это общекультурный предмет, который позволяет правильно ориентироваться в окружающей действительности и «ум в порядок приводить» Математика — необходимая часть гуманитарного знания общечеловеческой культуры. Умения анализировать, доказывать, сравнивать, обобщать — это метапредметные результаты обучения математике. Логическое, абстрактное, образное и пространственное виды мышлений развиваются непосредственно на уроках математики. Игра «МногогранникУм» позволит учащимся разных возрастов почувствовать себя в ситуации успеха на предмете математика, повысит интерес к изучению данного предмета, даст новые метапредметные знания и умения каждому участнику. При этом для участия в игре достаточно базового уровня предметных знаний.
Игра «МногогранникУм» позволит учащимся разных возрастов почувствовать себя в ситуации успеха на предмете математика, повысит интерес к изучению данного предмета, даст новые метапредметные знания и умения каждому участнику. При этом для участия в игре достаточно базового уровня предметных знаний.
Цель игры «МногогранникУм». Реализация сформированных у учащихся метапредметных навыков и компетенций.
Задачи игры «МногогранникУм»:
- развить произвольное внимание учащихся;
- развить память учащихся;
- развить логическое мышление учащихся;
- повысить мотивацию у учащихся к изучению математики;
- развить коммуникативные и регулятивные компетенции учащихся.
Планируемые результаты игры «МногогранникУм»:
- произвольное внимание учащихся развито на достаточном уровне;
- учащимся известны разнообразные техники запоминания формул, теорем и утверждений;
- учащиеся умеют работать в разновозрастной команде;
- учащиеся имеют опыт создания убедительной агрументации.

Участники: разновозрастные команды учащихся (4 человека: семиклассник, восьмиклассник, девятиклассник, десятиклассник).
Жюри: учителя, сопровождающие команды.
Подробный сценарий развивающей математической игры «МногогранникУм». Подробный сценарий развивающей игры «МногогранникУм» по географии.
математиков: Развитие математики | Infoplease
Самые ранние записи по математике показывают, что она возникла в ответ на практические потребности в сельском хозяйстве, бизнесе и промышленности. В Египте и Месопотамии, где свидетельства датируются 2 и 3 тысячелетиями до нашей эры, они использовались для съемки и измерения; оценки значения π (pi) находятся в обоих местах. Есть некоторые свидетельства аналогичных событий в Индии и Китае в тот же период, но сохранилось мало записей.Эта ранняя математика, как правило, эмпирическая, полученная методом проб и ошибок как лучший доступный способ получения результатов без каких-либо доказательств.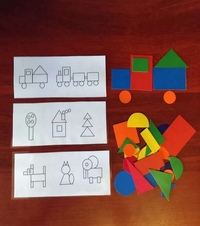 Однако теперь известно, что вавилоняне осознавали необходимость доказательств еще до греков, которые считались виновниками этого важного шага.
Однако теперь известно, что вавилоняне осознавали необходимость доказательств еще до греков, которые считались виновниками этого важного шага.
Глубокие изменения произошли в природе и подходе к математике благодаря вкладам греков. Более ранний (эллинский) период представлен Фалесом (VI в.До н.э.), Пифагора, Платона и Аристотеля, а также связанных с ними школ. Теорема Пифагора, известная ранее в Месопотамии, была открыта греками в этот период.
Во время Золотого века (V век до н.э.) Гиппократ Хиосский положил начало аксиоматическому подходу к геометрии, а Зенон Элейский предложил свои знаменитые парадоксы, касающиеся бесконечного и бесконечно малого, подняв вопросы о природе точек и взаимосвязях между ними. , строки и числа. Открытие с помощью геометрии иррациональных чисел, таких как 2, также относится к этому периоду.Евдокс Книдский (4 в. До н. Э.) Решил некоторые проблемы, предложив методы, альтернативные методам, связанным с бесконечно малыми; он известен своей работой над геометрическими пропорциями и своей теорией истощения для определения площадей и объемов.
Поздний (эллинистический) период греческой науки связан со школой Александрии. Величайший труд греческой математики, « элементов » Евклида (около 300 г. до н.э.), появился в начале этого периода. Элементарная геометрия, преподаваемая в средней школе, все еще в значительной степени основана на презентации Евклида, которая послужила моделью для дедуктивных систем в других частях математики и других наук.В этом методе сначала определяются примитивные термины, такие как point и line, , затем без доказательства формулируются определенные аксиомы и постулаты, относящиеся к ним и кажущиеся прямо вытекающими из них; затем ряд утверждений выводится путем дедукции из определений, аксиом и постулатов. Евклид также внес вклад в развитие арифметики и представил геометрическую теорию квадратных уравнений.
В III в. До н.э., Архимед, в дополнение к своей работе в области механики, сделал оценку π и использовал теорию исчерпания Евдокса для получения результатов, которые предвещали гораздо более поздние результаты интегрального исчисления, а Аполлоний Пергский назвал конические сечения и дал первую теорию для них. Вторая александрийская школа римского периода включала вклад Менелая (около 100 г. н.э., сферические треугольники), Герона Александрийского (геометрия), Птолемея (150 г. н.э., астрономия, геометрия, картография), Паппа (3-й век, геометрия), и Диофант (3-й век, арифметика).
Вторая александрийская школа римского периода включала вклад Менелая (около 100 г. н.э., сферические треугольники), Герона Александрийского (геометрия), Птолемея (150 г. н.э., астрономия, геометрия, картография), Паппа (3-й век, геометрия), и Диофант (3-й век, арифметика).
Вслед за упадком обучения на Западе после III в. Развитие математики продолжилось и на Востоке. В Китае Цу Чун-Чжи оценивал π по вписанным и описанным многоугольникам, как это сделал Архимед, а в Индии числа, которые сейчас используются во всем цивилизованном мире, были изобретены, а вклад в геометрию внесли Арьябхата и Брахмагупта (V и VI вв. .ОБЪЯВЛЕНИЕ). Арабы несли ответственность за сохранение работы греков, которую они переводили, комментировали и дополняли. В Багдаде Аль-Ховаризми (IX век) написал важную работу по алгебре и впервые представил на Западе индусские цифры, а Аль-Баттани работал над тригонометрией. В Египте Ибн аль-Хайсам интересовался телами вращения и геометрической оптикой. Персидский поэт Омар Хайям писал по алгебре.
Слово о китайских и ближневосточных произведениях начало доходить до Запада в 12 и 13 веках.Одним из первых крупных математиков Европы был Леонардо да Пиза (Леонардо Фибоначчи), писавший по арифметике и алгебре ( Liber abaci, 1202) и по геометрии ( Practica geometriae, 1220). С эпохой Возрождения резко возродился интерес к обучению, и изобретение книгопечатания сделало многие из ранних книг широко доступными. К концу 16 в. успехи были сделаны в алгебре Никколо Тарталья и Джироламо Кардано, в тригонометрии Франсуа Вьете и в таких областях прикладной математики, как картографирование Меркатором и другими.
Однако в 17 веке в математике произошла величайшая революция, поскольку научная революция распространилась на все области. Десятичные дроби были изобретены Саймоном Стевином, а логарифмы — Джоном Нэпиром и Генри Бриггсом; начала проективной геометрии положили Жерар Дезарг и Блез Паскаль; теория чисел была значительно расширена Пьером де Ферма; а теория вероятностей была основана Паскалем, Ферма и другими. В применении математики к механике и астрономии фундаментальный вклад внесли Галилей и Иоганнес Кеплер.
В применении математики к механике и астрономии фундаментальный вклад внесли Галилей и Иоганнес Кеплер.
Однако величайшим математическим достижением 17 века было изобретение аналитической геометрии Рене Декартом и исчисления Исааком Ньютоном и, независимо, Г. В. Лейбницем. Изобретение Декарта (предвосхищенное Ферма, чья работа была опубликована позже) сделало возможным выражение геометрических проблем в алгебраической форме и наоборот. Он был незаменим при создании исчисления, которое основывалось на и вытесняло более ранние специальные методы нахождения площадей, объемов и касательных к кривым, разработанные Ф.Б. Кавальери, Ферма и другие. Исчисление, вероятно, является величайшим инструментом из когда-либо изобретенных для математической постановки и решения физических проблем.
История математики XVIII в. доминирует развитие методов исчисления и их применение к таким задачам, как земным, так и небесным, с ведущими ролями, которые играют семья Бернулли (особенно Якоб, Иоганн и Даниэль), Леонард Эйлер, Гийом де Л’Опиталь. , и Ж.Л. Лагранж.Важные успехи в геометрии начались к концу века с работ Гаспара Монжа по начертательной геометрии и дифференциальной геометрии и продолжились благодаря его влиянию на других, например, его ученика Ж. В. Понселе, основавшего проективную геометрию (1822).
, и Ж.Л. Лагранж.Важные успехи в геометрии начались к концу века с работ Гаспара Монжа по начертательной геометрии и дифференциальной геометрии и продолжились благодаря его влиянию на других, например, его ученика Ж. В. Понселе, основавшего проективную геометрию (1822).
Современный период математики датируется началом 19 века, и его доминирующей фигурой является К. Ф. Гаусс. В области геометрии Гаусс внес фундаментальный вклад в дифференциальную геометрию, много сделал для открытия того, что сначала называлось Analysis situs, но теперь называется топологией, и предвосхитил (хотя он не публиковал свои результаты) великий прорыв в неевклидовой геометрии.Этот прорыв был сделан Н. И. Лобачевским (1826 г.) и независимо от него Яношом Бойяи (1832 г.), сыном близкого друга Гаусса, каждый из которых установил независимость пятого (параллельного) постулата Евклида и показал, что разные, самостоятельные непротиворечивая геометрия может быть получена путем замены ее другим постулатом. Еще одна неевклидова геометрия была изобретена Бернхардом Риманом (1854 г. ), работа которого также заложила основы современного тензорного исчисления для описания пространства, столь важного для общей теории относительности.
), работа которого также заложила основы современного тензорного исчисления для описания пространства, столь важного для общей теории относительности.
В области арифметики, теории чисел и алгебры Гаусс снова лидировал. Он основал современную теорию чисел, дал первое ясное изложение комплексных чисел и исследовал функции комплексных переменных. Понятие числа было далее расширено У. Р. Гамильтоном, чья теория кватернионов (1843 г.) предоставила первый пример некоммутативной алгебры (то есть такой, в которой ab ≠ ba). Эта работа была обобщена в следующем году Г. Г. Грассманом, который показал, что несколько различных согласованных алгебр могут быть получены путем выбора различных наборов аксиом, управляющих операциями над элементами алгебры.
Эти разработки продолжились в теории групп М. С. Ли в конце 19 века. и достиг полного выражения в широком диапазоне современной абстрактной алгебры. Теория чисел получила значительный вклад во второй половине XIX века. через работы Георга Кантора, Дж. В. Р. Дедекинда и К. В. Вейерштрасса. Еще одним влиянием Гаусса было его настойчивое требование строгих доказательств во всех областях математики. В ходе анализа это тщательное изучение основ исчисления привело к тому, что А.Теория пределов Л. Коши (1821 г.), которая, в свою очередь, дала новые и более четкие определения непрерывности, производной и определенного интеграла. Еще один важный шаг к строгости был сделан Вейерштрассом, который поднял новые вопросы об этих концепциях и показал, что в конечном итоге основы анализа зиждутся на свойствах действительной системы счисления.
В. Р. Дедекинда и К. В. Вейерштрасса. Еще одним влиянием Гаусса было его настойчивое требование строгих доказательств во всех областях математики. В ходе анализа это тщательное изучение основ исчисления привело к тому, что А.Теория пределов Л. Коши (1821 г.), которая, в свою очередь, дала новые и более четкие определения непрерывности, производной и определенного интеграла. Еще один важный шаг к строгости был сделан Вейерштрассом, который поднял новые вопросы об этих концепциях и показал, что в конечном итоге основы анализа зиждутся на свойствах действительной системы счисления.
В 20 в. тенденция заключалась в увеличении обобщения и абстракции, при этом элементы и операции систем определялись настолько широко, что их интерпретации связывали такие области, как алгебра, геометрия и топология.Ключом к этому подходу было использование формальной аксиоматики, в которой было отброшено понятие аксиом как самоочевидных истин
. Вместо этого упор был сделан на такие логические понятия, как последовательность и полнота. Корни формальной аксиоматики лежат в открытиях альтернативных систем геометрии и алгебры в 19 веке; Впервые этот подход был систематически применен Давидом Гильбертом в его работе по основам геометрии (1899 г.).
Корни формальной аксиоматики лежат в открытиях альтернативных систем геометрии и алгебры в 19 веке; Впервые этот подход был систематически применен Давидом Гильбертом в его работе по основам геометрии (1899 г.).
Акцент на дедуктивной логике, присущий этому взгляду на математику, и открытие взаимосвязей между различными разделами математики и их основной основы в теории чисел привели к активной деятельности в области математической логики на рубеже веков.Конкурирующие школы мысли выросли под руководством Гильберта, Бертрана Рассела, А. Н. Уайтхеда и Л. Э. Дж. Брауэра. Важный вклад в исследование логических основ математики внесли Курт Гёдель и А. Черч.
Колумбийская электронная энциклопедия, 6-е изд. Авторское право © 2012, Columbia University Press. Все права защищены.
См. Другие статьи в энциклопедии по следующим темам: Математика
Помогите вашему ребенку развить ранние математические навыки • НУЛЬ ДО ТРЕХ
Дети используют первые математические навыки в повседневных делах и занятиях. Это хорошая новость, поскольку эти навыки важны для подготовки к школе. Но ранняя математика не означает вынимать калькулятор во время игры. Еще до того, как они пойдут в школу, большинство детей развивают понимание сложения и вычитания посредством повседневного взаимодействия. Например, у Томаса две машины; Джозеф хочет один. После того, как Томас поделился одной, он видит, что у него осталась одна машина (Bowman, Donovan, & Burns, 2001, p. 201). Другие математические навыки приобретаются в ходе повседневных занятий, которыми вы делитесь со своим ребенком, например, с подсчетом шагов по мере того, как вы поднимаетесь или опускаетесь.Неформальные занятия, подобные этой, дают детям толчок к формальному обучению математике, которое начинается в школе.
Это хорошая новость, поскольку эти навыки важны для подготовки к школе. Но ранняя математика не означает вынимать калькулятор во время игры. Еще до того, как они пойдут в школу, большинство детей развивают понимание сложения и вычитания посредством повседневного взаимодействия. Например, у Томаса две машины; Джозеф хочет один. После того, как Томас поделился одной, он видит, что у него осталась одна машина (Bowman, Donovan, & Burns, 2001, p. 201). Другие математические навыки приобретаются в ходе повседневных занятий, которыми вы делитесь со своим ребенком, например, с подсчетом шагов по мере того, как вы поднимаетесь или опускаетесь.Неформальные занятия, подобные этой, дают детям толчок к формальному обучению математике, которое начинается в школе.
Какие математические знания понадобятся вашему ребенку в начальной школе? Ранние математические концепции и навыки, которые используются в учебной программе по математике в первом классе, включают: (Bowman et al., 2001, p. 76).
Размер, форма и узоры
Умение считать вербально (сначала вперед, потом назад)
Распознавающие цифры
Определение большего и меньшего количества
Понимание однозначной корреспонденции (т.
 е., сопоставление наборов или знание, в какой группе их четыре, а в какой пять)
е., сопоставление наборов или знание, в какой группе их четыре, а в какой пять)
Ключевые математические навыки для школы
Более продвинутые математические навыки основаны на начальном математическом «фундаменте» — точно так же, как дом построен на прочном фундаменте. В первые годы жизни вы можете помочь своему ребенку начать развивать математические навыки в раннем возрасте, представив такие идеи, как: (Из Diezmann & Yelland, 2000 и Fromboluti & Rinck, 1999.)
Смысл числа
Это умение точно считать — первый нападающий.Затем, позже в школе, дети научатся считать в обратном порядке. Более сложный навык, связанный с чувством чисел, — это способность видеть отношения между числами, например, сложение и вычитание. Бен (2 года) увидел кексы на тарелке. Он сосчитал со своим отцом: «Один, два, три, четыре, пять, шесть… »
Представительство
Реализация математических идей с помощью слов, картинок, символов и предметов (например, блоков).![]() Кейси (3 года) собирался на пикник. Он аккуратно разложил четыре пластмассовые тарелки и четыре пластмассовых стакана: «Так что всей семьей приехать на пикник!» В его семье было четыре члена; он смог применить эту информацию к выбранному количеству тарелок и чашек.
Кейси (3 года) собирался на пикник. Он аккуратно разложил четыре пластмассовые тарелки и четыре пластмассовых стакана: «Так что всей семьей приехать на пикник!» В его семье было четыре члена; он смог применить эту информацию к выбранному количеству тарелок и чашек.
Пространственное чувство
Позже в школе дети будут называть это «геометрией». Но для малышей он знакомит с идеями формы, размера, пространства, положения, направления и движения. Азиз (28 месяцев) хихикал внизу слайда. «Что тут смешного?» — недоумевала его тетя. «Я поднялся, — сказал Азиз, — а потом спустился!»
Измерение
Технически это определение длины, высоты и веса объекта в таких единицах, как дюймы, футы или фунты.Измерение времени (например, в минутах) также относится к этой области навыков. Габриэлла (36 месяцев) снова и снова спрашивала свою Абуэлу: «Сделать печенье? Я сделаю это! » Ее Абуэла показала ей, как наполнить мерный стакан сахаром. «Нам нужны две чашки, Габи. Наполните его один раз и положите в миску, а затем снова наполните ».
Наполните его один раз и положите в миску, а затем снова наполните ».
Оценка
Это способность сделать хорошее предположение о количестве или размере чего-либо. Маленьким детям это сделать очень сложно.Вы можете помочь им, показав им значение таких слов, как больше, меньше, больше, меньше, больше чем, меньше чем. Нолан (30 месяцев) посмотрел на два рогалика: один был обычным, другой — мини-бубликом. Его отец спросил: «Какой из них ты предпочитаешь?» Нолан указал на обычный рогалик. Его отец сказал: «Ты, должно быть, голоден! Этот рогалик больше. Этот бублик меньше. Хорошо, я дам тебе большую. Скоро завтрак! »
Узоры
Узоры — это вещи, числа, формы, изображения, которые логически повторяются.Шаблоны помогают детям научиться делать прогнозы, понимать, что будет дальше, устанавливать логические связи и использовать навыки рассуждения. Ава (27 месяцев) указала на Луну: «Луна. Солнце переходит ночь-ночь. Дедушка подобрал ее: «Да, маленькая Ава. Утром выходит солнце, а луна уходит. Ночью солнце засыпает, а луна выходит играть. Но пора Аве спать, прямо как солнце.
Утром выходит солнце, а луна уходит. Ночью солнце засыпает, а луна выходит играть. Но пора Аве спать, прямо как солнце.
Решение проблем
Способность продумать проблему, признать, что к ответу существует более одного пути.Это означает использование прошлых знаний и навыков логического мышления для поиска ответа. Карл (15 месяцев) посмотрел на сортировщик формы — пластиковый барабан с тремя отверстиями в верхней части. Отверстия имели форму треугольника, круга и квадрата. Карл посмотрел на массивные фигуры на полу. Он поднял треугольник. Он положил его в свой месяц, а затем ударил им об пол. Он коснулся краев пальцами. Затем он попытался засунуть его в каждую дырочку новой игрушки. Сюрприз! Он упал в отверстие треугольника! Карл потянулся к другому блоку, на этот раз круглому…
Математика: одна часть целого
Математические навыки — это лишь часть более широкой сети навыков, которые дети развивают в ранние годы, включая языковые, физические и социальные навыки.Каждая из этих областей навыков зависит от других и влияет на них.
Трина (18 месяцев) укладывала блоки. Она положила два квадратных блока один на другой, а затем треугольный. Она обнаружила, что никакие блоки больше не будут балансировать на вершине блока треугольной формы. Она взглянула на своего отца и показала ему блок, который ей не удалось преодолеть, чтобы оставаться на вершине, по сути говоря ему жестом: «Папа, мне нужна помощь, чтобы разобраться в этом». Ее отец показал ей, что, если она снимет треугольный блок и вместо него возьмет квадратный, она сможет сложить еще больше.Затем она добавила еще два блока к своей башне, прежде чем с гордостью показать свое творение отцу: «Дада, Оок! Оу! »
В этом обычном взаимодействии вы можете увидеть, как все области разработки Trina работают вместе. Ее физические способности позволяют ей манипулировать блоками и использовать свои мыслительные способности для выполнения своего плана по постройке башни. Она использует свой язык и социальные навыки, когда просит помощи у отца. Ее эффективное общение позволяет отцу реагировать и оказывать необходимую помощь (дальнейшее развитие ее социальных навыков, поскольку она считает себя важным и хорошим коммуникатором).Это еще больше укрепляет ее мыслительные способности, поскольку она узнает, как решить проблему увеличения высоты башни.
Что вы можете сделать
Приведенные ниже советы показывают, как вы можете помочь своему ребенку освоить математические навыки в раннем возрасте, опираясь на его природное любопытство и весело проводя время вместе. (Примечание: большинство этих советов предназначены для детей старшего возраста — в возрасте от 2 до 3 лет. Дети младшего возраста могут быть представлены рассказам и песням, используя повторение, рифмы и числа.)
Поднимайся.
Играть с сортировщиками формы. Поговорите с ребенком о каждой форме — посчитайте стороны, опишите цвета. Создавайте свои собственные фигуры, вырезая большие фигуры из цветной плотной бумаги. Попросите ребенка «прыгнуть по кругу» или «запрыгнуть на красную фигуру».
Подсчитайте и отсортируйте.
Соберите корзину с маленькими игрушками, ракушками, камешками или пуговицами. Считайте их вместе с ребенком. Отсортируйте их по размеру, цвету или назначению (то есть все машины в одной стопке, все животные в другой).
Сделайте звонок.
Вместе со своей 3-летней дочкой начните учить ее адрес и номер телефона своего дома. Поговорите с ребенком о том, что у каждого дома есть номер, и как его дом или квартира входят в серию, каждая со своим номером.
Какой это размер?
Обратите внимание на размеры объектов в мире вокруг вас: этот розовый бумажник самый большой. Синий кошелек самый маленький. Попросите ребенка подумать о своем размере по сравнению с другими предметами («Вы помещаетесь под столом? Под стулом?»).
Теперь ты готовишь!
Наполнять, перемешивать и наливать могут даже маленькие дети. Благодаря этим упражнениям дети естественным образом учатся считать, измерять, складывать и оценивать.
Уходи прочь.
Прогулка дает детям множество возможностей сравнить (какой камень больше?), Оценить (сколько желудей мы нашли?), Отметить сходства и различия (есть ли у утки мех, как у кролика?) И распределить по категориям (посмотреть, есть ли у утки мех, как у кролика?) можно найти красные листья). Вы также можете поговорить о размере (делая большие и маленькие шаги), оценить расстояние (парк рядом с нашим домом или далеко?) И потренироваться в счете (давайте посчитаем, сколько шагов мы дойдем до угла).
Время картинки.
Используйте песочные часы, секундомер или таймер для коротких (1–3 минут) занятий. Это помогает детям развить чувство времени и понять, что на одни дела уходит больше времени, чем на другие.
Поднимайся.
Укажите на разные формы и цвета, которые вы видите в течение дня. Во время прогулки вы можете увидеть знак в форме треугольника желтого цвета. Внутри магазина вы можете увидеть красный прямоугольник.
Прочтите и пой свои числа.
Пойте рифмующиеся, повторяющиеся или содержащие числа песни.Песни закрепляют закономерности (что тоже является математическим навыком). Они также являются интересным способом попрактиковаться в языке и развить такие социальные навыки, как сотрудничество.
Начни сегодня.
Используйте календарь, чтобы говорить о дате, дне недели и погоде. Календари усиливают подсчет, последовательности и закономерности. Развивайте навыки логического мышления, говоря о холодной погоде и спрашивая ребенка: что мы надеваем, когда холодно? Это побуждает вашего ребенка находить связь между холодной погодой и теплой одеждой.
Раздать.
Попросите вашего ребенка помочь в распределении таких предметов, как закуски, или в разложении салфеток на обеденном столе. Помогите ему дать каждому ребенку по крекеру. Это помогает детям понимать индивидуальную переписку. Когда вы раздаете предметы, подчеркните концепцию числа: «Один для вас, один для меня, один для папы». Или: «Мы надеваем обувь: раз, два».
Большой на блоках.
Дайте вашему ребенку возможность поиграть с деревянными блоками, пластиковыми блокировками, пустыми коробками, пакетами из-под молока и т. Д.Сложение этих игрушек в стопку и манипулирование ими помогает детям узнать о формах и отношениях между формами (например, два треугольника образуют квадрат). Скворечники и чашки для детей младшего возраста помогают им понять взаимосвязь между объектами разного размера.
Время туннеля.
Откройте большие картонные коробки с каждого конца, чтобы превратить их в туннель. Это помогает детям понять, где находится их тело в пространстве и по отношению к другим объектам.
Длинное и короткое.
Отрежьте несколько (3-5) кусочков ленты, пряжи или бумаги разной длины. Говорите о таких идеях, как длинные и короткие. Расположите ребенка в порядке от самого длинного к самому короткому.
Учитесь на ощупь.
Вырежьте фигуры — круг, квадрат, треугольник — из прочного картона. Пусть ваш ребенок коснется фигуры открытыми, а затем закрытыми глазами.
Образец воспроизведения.
Развлекайтесь с выкройками, позволяя детям раскладывать сухие макароны, крупные бусины, разные виды сухих хлопьев или кусочки бумаги разными узорами или рисунками.Во время этого занятия внимательно следите за ребенком, чтобы не подавиться, и уберите все предметы, когда закончите.
Обучение стирке.
Сделайте работу по дому интересной. Сортируя белье, попросите ребенка сделать стопку рубашек и стопку носков. Спросите его, какая стопка больше (оценка). Вместе посчитайте, сколько рубашек. Посмотрите, сможет ли он сделать пары носков: вы можете вынуть два носка и сложить их в стопку? (Не беспокойтесь, если они не совпадают! Это упражнение больше связано с подсчетом, чем с сопоставлением.)
Детская площадка по математике.
Пока ваш ребенок играет, сравнивайте его по росту (высокий / низкий), положению (больше / меньше) или размеру (большой / маленький).
Платье для успеха в математике.
Попросите ребенка выбрать рубашку на день. Спросите: Какого цвета ваша рубашка? Да, желтый. Можете ли вы найти в своей комнате что-нибудь желтое? Когда вашему ребенку исполнится три года и больше, обратите внимание на узоры на его одежде — например, полосы, цвета, формы или изображения: я вижу узор на вашей рубашке.Есть полосы, которые идут красным, синим, красным, синим. Или, ваша рубашка покрыта пони — большой пони рядом с маленьким пони, по всей вашей рубашке!
Графические игры.
Когда вашему ребенку исполнится три года и больше, составьте таблицу, на которой он сможет наклеивать стикер каждый раз, когда идет дождь или каждый раз, когда солнечно. В конце недели вы можете вместе прикинуть, в каком столбце больше или меньше наклеек, и подсчитать, сколько, чтобы быть уверенным.
Список литературы
Боуман, Б.Т., Донован М.С. и Бернс М.С. (ред.). (2001). Стремятся учиться: обучение наших дошкольников. Вашингтон, округ Колумбия: Национальная академия наук.
Diezmann, C., & Yelland, N.J. (2000). Развитие математической грамотности в раннем детстве. В Йелланде, штат Нью-Джерси (ред.), Содействие осмысленному обучению: инновации в обучении профессионалов дошкольного образования. (стр.47–58). Вашингтон, округ Колумбия: Национальная ассоциация образования детей младшего возраста.
Фромболути, К.С. и Ринк Н. (1999, июнь). Раннее детство: где начинается обучение. Министерство образования США, Управление исследований и совершенствования образования, Национальный институт развития и образования детей младшего возраста. Получено 11 мая 2018 г. по адресу https://www2.ed.gov/pubs/EarlyMath/title.html
.Помогите вашему ребенку развить ранние математические навыки • НОЛЬ ДО ТРЕХ
Дети используют первые математические навыки в повседневных делах и занятиях.Это хорошая новость, поскольку эти навыки важны для подготовки к школе. Но ранняя математика не означает вынимать калькулятор во время игры. Еще до того, как они пойдут в школу, большинство детей развивают понимание сложения и вычитания посредством повседневного взаимодействия. Например, у Томаса две машины; Джозеф хочет один. После того, как Томас поделился одной, он видит, что у него осталась одна машина (Bowman, Donovan, & Burns, 2001, p. 201). Другие математические навыки приобретаются в ходе повседневных занятий, которыми вы делитесь со своим ребенком, например, с подсчетом шагов по мере того, как вы поднимаетесь или опускаетесь.Неформальные занятия, подобные этой, дают детям толчок к формальному обучению математике, которое начинается в школе.
Какие математические знания понадобятся вашему ребенку в начальной школе? Ранние математические концепции и навыки, которые используются в учебной программе по математике в первом классе, включают: (Bowman et al., 2001, p. 76).
Размер, форма и узоры
Умение считать вербально (сначала вперед, потом назад)
Распознавающие цифры
Определение большего и меньшего количества
Понимание однозначной корреспонденции (т.е., сопоставление наборов или знание, в какой группе их четыре, а в какой пять)
Ключевые математические навыки для школы
Более продвинутые математические навыки основаны на начальном математическом «фундаменте» — точно так же, как дом построен на прочном фундаменте. В первые годы жизни вы можете помочь своему ребенку начать развивать математические навыки в раннем возрасте, представив такие идеи, как: (Из Diezmann & Yelland, 2000 и Fromboluti & Rinck, 1999.)
Смысл числа
Это умение точно считать — первый нападающий.Затем, позже в школе, дети научатся считать в обратном порядке. Более сложный навык, связанный с чувством чисел, — это способность видеть отношения между числами, например, сложение и вычитание. Бен (2 года) увидел кексы на тарелке. Он сосчитал со своим отцом: «Один, два, три, четыре, пять, шесть… »
Представительство
Реализация математических идей с помощью слов, картинок, символов и предметов (например, блоков). Кейси (3 года) собирался на пикник. Он аккуратно разложил четыре пластмассовые тарелки и четыре пластмассовых стакана: «Так что всей семьей приехать на пикник!» В его семье было четыре члена; он смог применить эту информацию к выбранному количеству тарелок и чашек.
Пространственное чувство
Позже в школе дети будут называть это «геометрией». Но для малышей он знакомит с идеями формы, размера, пространства, положения, направления и движения. Азиз (28 месяцев) хихикал внизу слайда. «Что тут смешного?» — недоумевала его тетя. «Я поднялся, — сказал Азиз, — а потом спустился!»
Измерение
Технически это определение длины, высоты и веса объекта в таких единицах, как дюймы, футы или фунты.Измерение времени (например, в минутах) также относится к этой области навыков. Габриэлла (36 месяцев) снова и снова спрашивала свою Абуэлу: «Сделать печенье? Я сделаю это! » Ее Абуэла показала ей, как наполнить мерный стакан сахаром. «Нам нужны две чашки, Габи. Наполните его один раз и положите в миску, а затем снова наполните ».
Оценка
Это способность сделать хорошее предположение о количестве или размере чего-либо. Маленьким детям это сделать очень сложно.Вы можете помочь им, показав им значение таких слов, как больше, меньше, больше, меньше, больше чем, меньше чем. Нолан (30 месяцев) посмотрел на два рогалика: один был обычным, другой — мини-бубликом. Его отец спросил: «Какой из них ты предпочитаешь?» Нолан указал на обычный рогалик. Его отец сказал: «Ты, должно быть, голоден! Этот рогалик больше. Этот бублик меньше. Хорошо, я дам тебе большую. Скоро завтрак! »
Узоры
Узоры — это вещи, числа, формы, изображения, которые логически повторяются.Шаблоны помогают детям научиться делать прогнозы, понимать, что будет дальше, устанавливать логические связи и использовать навыки рассуждения. Ава (27 месяцев) указала на Луну: «Луна. Солнце переходит ночь-ночь. Дедушка подобрал ее: «Да, маленькая Ава. Утром выходит солнце, а луна уходит. Ночью солнце засыпает, а луна выходит играть. Но пора Аве спать, прямо как солнце.
Решение проблем
Способность продумать проблему, признать, что к ответу существует более одного пути.Это означает использование прошлых знаний и навыков логического мышления для поиска ответа. Карл (15 месяцев) посмотрел на сортировщик формы — пластиковый барабан с тремя отверстиями в верхней части. Отверстия имели форму треугольника, круга и квадрата. Карл посмотрел на массивные фигуры на полу. Он поднял треугольник. Он положил его в свой месяц, а затем ударил им об пол. Он коснулся краев пальцами. Затем он попытался засунуть его в каждую дырочку новой игрушки. Сюрприз! Он упал в отверстие треугольника! Карл потянулся к другому блоку, на этот раз круглому…
Математика: одна часть целого
Математические навыки — это лишь часть более широкой сети навыков, которые дети развивают в ранние годы, включая языковые, физические и социальные навыки.Каждая из этих областей навыков зависит от других и влияет на них.
Трина (18 месяцев) укладывала блоки. Она положила два квадратных блока один на другой, а затем треугольный. Она обнаружила, что никакие блоки больше не будут балансировать на вершине блока треугольной формы. Она взглянула на своего отца и показала ему блок, который ей не удалось преодолеть, чтобы оставаться на вершине, по сути говоря ему жестом: «Папа, мне нужна помощь, чтобы разобраться в этом». Ее отец показал ей, что, если она снимет треугольный блок и вместо него возьмет квадратный, она сможет сложить еще больше.Затем она добавила еще два блока к своей башне, прежде чем с гордостью показать свое творение отцу: «Дада, Оок! Оу! »
В этом обычном взаимодействии вы можете увидеть, как все области разработки Trina работают вместе. Ее физические способности позволяют ей манипулировать блоками и использовать свои мыслительные способности для выполнения своего плана по постройке башни. Она использует свой язык и социальные навыки, когда просит помощи у отца. Ее эффективное общение позволяет отцу реагировать и оказывать необходимую помощь (дальнейшее развитие ее социальных навыков, поскольку она считает себя важным и хорошим коммуникатором).Это еще больше укрепляет ее мыслительные способности, поскольку она узнает, как решить проблему увеличения высоты башни.
Что вы можете сделать
Приведенные ниже советы показывают, как вы можете помочь своему ребенку освоить математические навыки в раннем возрасте, опираясь на его природное любопытство и весело проводя время вместе. (Примечание: большинство этих советов предназначены для детей старшего возраста — в возрасте от 2 до 3 лет. Дети младшего возраста могут быть представлены рассказам и песням, используя повторение, рифмы и числа.)
Поднимайся.
Играть с сортировщиками формы. Поговорите с ребенком о каждой форме — посчитайте стороны, опишите цвета. Создавайте свои собственные фигуры, вырезая большие фигуры из цветной плотной бумаги. Попросите ребенка «прыгнуть по кругу» или «запрыгнуть на красную фигуру».
Подсчитайте и отсортируйте.
Соберите корзину с маленькими игрушками, ракушками, камешками или пуговицами. Считайте их вместе с ребенком. Отсортируйте их по размеру, цвету или назначению (то есть все машины в одной стопке, все животные в другой).
Сделайте звонок.
Вместе со своей 3-летней дочкой начните учить ее адрес и номер телефона своего дома. Поговорите с ребенком о том, что у каждого дома есть номер, и как его дом или квартира входят в серию, каждая со своим номером.
Какой это размер?
Обратите внимание на размеры объектов в мире вокруг вас: этот розовый бумажник самый большой. Синий кошелек самый маленький. Попросите ребенка подумать о своем размере по сравнению с другими предметами («Вы помещаетесь под столом? Под стулом?»).
Теперь ты готовишь!
Наполнять, перемешивать и наливать могут даже маленькие дети. Благодаря этим упражнениям дети естественным образом учатся считать, измерять, складывать и оценивать.
Уходи прочь.
Прогулка дает детям множество возможностей сравнить (какой камень больше?), Оценить (сколько желудей мы нашли?), Отметить сходства и различия (есть ли у утки мех, как у кролика?) И распределить по категориям (посмотреть, есть ли у утки мех, как у кролика?) можно найти красные листья). Вы также можете поговорить о размере (делая большие и маленькие шаги), оценить расстояние (парк рядом с нашим домом или далеко?) И потренироваться в счете (давайте посчитаем, сколько шагов мы дойдем до угла).
Время картинки.
Используйте песочные часы, секундомер или таймер для коротких (1–3 минут) занятий. Это помогает детям развить чувство времени и понять, что на одни дела уходит больше времени, чем на другие.
Поднимайся.
Укажите на разные формы и цвета, которые вы видите в течение дня. Во время прогулки вы можете увидеть знак в форме треугольника желтого цвета. Внутри магазина вы можете увидеть красный прямоугольник.
Прочтите и пой свои числа.
Пойте рифмующиеся, повторяющиеся или содержащие числа песни.Песни закрепляют закономерности (что тоже является математическим навыком). Они также являются интересным способом попрактиковаться в языке и развить такие социальные навыки, как сотрудничество.
Начни сегодня.
Используйте календарь, чтобы говорить о дате, дне недели и погоде. Календари усиливают подсчет, последовательности и закономерности. Развивайте навыки логического мышления, говоря о холодной погоде и спрашивая ребенка: что мы надеваем, когда холодно? Это побуждает вашего ребенка находить связь между холодной погодой и теплой одеждой.
Раздать.
Попросите вашего ребенка помочь в распределении таких предметов, как закуски, или в разложении салфеток на обеденном столе. Помогите ему дать каждому ребенку по крекеру. Это помогает детям понимать индивидуальную переписку. Когда вы раздаете предметы, подчеркните концепцию числа: «Один для вас, один для меня, один для папы». Или: «Мы надеваем обувь: раз, два».
Большой на блоках.
Дайте вашему ребенку возможность поиграть с деревянными блоками, пластиковыми блокировками, пустыми коробками, пакетами из-под молока и т. Д.Сложение этих игрушек в стопку и манипулирование ими помогает детям узнать о формах и отношениях между формами (например, два треугольника образуют квадрат). Скворечники и чашки для детей младшего возраста помогают им понять взаимосвязь между объектами разного размера.
Время туннеля.
Откройте большие картонные коробки с каждого конца, чтобы превратить их в туннель. Это помогает детям понять, где находится их тело в пространстве и по отношению к другим объектам.
Длинное и короткое.
Отрежьте несколько (3-5) кусочков ленты, пряжи или бумаги разной длины. Говорите о таких идеях, как длинные и короткие. Расположите ребенка в порядке от самого длинного к самому короткому.
Учитесь на ощупь.
Вырежьте фигуры — круг, квадрат, треугольник — из прочного картона. Пусть ваш ребенок коснется фигуры открытыми, а затем закрытыми глазами.
Образец воспроизведения.
Развлекайтесь с выкройками, позволяя детям раскладывать сухие макароны, крупные бусины, разные виды сухих хлопьев или кусочки бумаги разными узорами или рисунками.Во время этого занятия внимательно следите за ребенком, чтобы не подавиться, и уберите все предметы, когда закончите.
Обучение стирке.
Сделайте работу по дому интересной. Сортируя белье, попросите ребенка сделать стопку рубашек и стопку носков. Спросите его, какая стопка больше (оценка). Вместе посчитайте, сколько рубашек. Посмотрите, сможет ли он сделать пары носков: вы можете вынуть два носка и сложить их в стопку? (Не беспокойтесь, если они не совпадают! Это упражнение больше связано с подсчетом, чем с сопоставлением.)
Детская площадка по математике.
Пока ваш ребенок играет, сравнивайте его по росту (высокий / низкий), положению (больше / меньше) или размеру (большой / маленький).
Платье для успеха в математике.
Попросите ребенка выбрать рубашку на день. Спросите: Какого цвета ваша рубашка? Да, желтый. Можете ли вы найти в своей комнате что-нибудь желтое? Когда вашему ребенку исполнится три года и больше, обратите внимание на узоры на его одежде — например, полосы, цвета, формы или изображения: я вижу узор на вашей рубашке.Есть полосы, которые идут красным, синим, красным, синим. Или, ваша рубашка покрыта пони — большой пони рядом с маленьким пони, по всей вашей рубашке!
Графические игры.
Когда вашему ребенку исполнится три года и больше, составьте таблицу, на которой он сможет наклеивать стикер каждый раз, когда идет дождь или каждый раз, когда солнечно. В конце недели вы можете вместе прикинуть, в каком столбце больше или меньше наклеек, и подсчитать, сколько, чтобы быть уверенным.
Список литературы
Боуман, Б.Т., Донован М.С. и Бернс М.С. (ред.). (2001). Стремятся учиться: обучение наших дошкольников. Вашингтон, округ Колумбия: Национальная академия наук.
Diezmann, C., & Yelland, N.J. (2000). Развитие математической грамотности в раннем детстве. В Йелланде, штат Нью-Джерси (ред.), Содействие осмысленному обучению: инновации в обучении профессионалов дошкольного образования. (стр.47–58). Вашингтон, округ Колумбия: Национальная ассоциация образования детей младшего возраста.
Фромболути, К.С. и Ринк Н. (1999, июнь). Раннее детство: где начинается обучение. Министерство образования США, Управление исследований и совершенствования образования, Национальный институт развития и образования детей младшего возраста. Получено 11 мая 2018 г. по адресу https://www2.ed.gov/pubs/EarlyMath/title.html
.Помогите вашему ребенку развить ранние математические навыки • НОЛЬ ДО ТРЕХ
Дети используют первые математические навыки в повседневных делах и занятиях.Это хорошая новость, поскольку эти навыки важны для подготовки к школе. Но ранняя математика не означает вынимать калькулятор во время игры. Еще до того, как они пойдут в школу, большинство детей развивают понимание сложения и вычитания посредством повседневного взаимодействия. Например, у Томаса две машины; Джозеф хочет один. После того, как Томас поделился одной, он видит, что у него осталась одна машина (Bowman, Donovan, & Burns, 2001, p. 201). Другие математические навыки приобретаются в ходе повседневных занятий, которыми вы делитесь со своим ребенком, например, с подсчетом шагов по мере того, как вы поднимаетесь или опускаетесь.Неформальные занятия, подобные этой, дают детям толчок к формальному обучению математике, которое начинается в школе.
Какие математические знания понадобятся вашему ребенку в начальной школе? Ранние математические концепции и навыки, которые используются в учебной программе по математике в первом классе, включают: (Bowman et al., 2001, p. 76).
Размер, форма и узоры
Умение считать вербально (сначала вперед, потом назад)
Распознавающие цифры
Определение большего и меньшего количества
Понимание однозначной корреспонденции (т.е., сопоставление наборов или знание, в какой группе их четыре, а в какой пять)
Ключевые математические навыки для школы
Более продвинутые математические навыки основаны на начальном математическом «фундаменте» — точно так же, как дом построен на прочном фундаменте. В первые годы жизни вы можете помочь своему ребенку начать развивать математические навыки в раннем возрасте, представив такие идеи, как: (Из Diezmann & Yelland, 2000 и Fromboluti & Rinck, 1999.)
Смысл числа
Это умение точно считать — первый нападающий.Затем, позже в школе, дети научатся считать в обратном порядке. Более сложный навык, связанный с чувством чисел, — это способность видеть отношения между числами, например, сложение и вычитание. Бен (2 года) увидел кексы на тарелке. Он сосчитал со своим отцом: «Один, два, три, четыре, пять, шесть… »
Представительство
Реализация математических идей с помощью слов, картинок, символов и предметов (например, блоков). Кейси (3 года) собирался на пикник. Он аккуратно разложил четыре пластмассовые тарелки и четыре пластмассовых стакана: «Так что всей семьей приехать на пикник!» В его семье было четыре члена; он смог применить эту информацию к выбранному количеству тарелок и чашек.
Пространственное чувство
Позже в школе дети будут называть это «геометрией». Но для малышей он знакомит с идеями формы, размера, пространства, положения, направления и движения. Азиз (28 месяцев) хихикал внизу слайда. «Что тут смешного?» — недоумевала его тетя. «Я поднялся, — сказал Азиз, — а потом спустился!»
Измерение
Технически это определение длины, высоты и веса объекта в таких единицах, как дюймы, футы или фунты.Измерение времени (например, в минутах) также относится к этой области навыков. Габриэлла (36 месяцев) снова и снова спрашивала свою Абуэлу: «Сделать печенье? Я сделаю это! » Ее Абуэла показала ей, как наполнить мерный стакан сахаром. «Нам нужны две чашки, Габи. Наполните его один раз и положите в миску, а затем снова наполните ».
Оценка
Это способность сделать хорошее предположение о количестве или размере чего-либо. Маленьким детям это сделать очень сложно.Вы можете помочь им, показав им значение таких слов, как больше, меньше, больше, меньше, больше чем, меньше чем. Нолан (30 месяцев) посмотрел на два рогалика: один был обычным, другой — мини-бубликом. Его отец спросил: «Какой из них ты предпочитаешь?» Нолан указал на обычный рогалик. Его отец сказал: «Ты, должно быть, голоден! Этот рогалик больше. Этот бублик меньше. Хорошо, я дам тебе большую. Скоро завтрак! »
Узоры
Узоры — это вещи, числа, формы, изображения, которые логически повторяются.Шаблоны помогают детям научиться делать прогнозы, понимать, что будет дальше, устанавливать логические связи и использовать навыки рассуждения. Ава (27 месяцев) указала на Луну: «Луна. Солнце переходит ночь-ночь. Дедушка подобрал ее: «Да, маленькая Ава. Утром выходит солнце, а луна уходит. Ночью солнце засыпает, а луна выходит играть. Но пора Аве спать, прямо как солнце.
Решение проблем
Способность продумать проблему, признать, что к ответу существует более одного пути.Это означает использование прошлых знаний и навыков логического мышления для поиска ответа. Карл (15 месяцев) посмотрел на сортировщик формы — пластиковый барабан с тремя отверстиями в верхней части. Отверстия имели форму треугольника, круга и квадрата. Карл посмотрел на массивные фигуры на полу. Он поднял треугольник. Он положил его в свой месяц, а затем ударил им об пол. Он коснулся краев пальцами. Затем он попытался засунуть его в каждую дырочку новой игрушки. Сюрприз! Он упал в отверстие треугольника! Карл потянулся к другому блоку, на этот раз круглому…
Математика: одна часть целого
Математические навыки — это лишь часть более широкой сети навыков, которые дети развивают в ранние годы, включая языковые, физические и социальные навыки.Каждая из этих областей навыков зависит от других и влияет на них.
Трина (18 месяцев) укладывала блоки. Она положила два квадратных блока один на другой, а затем треугольный. Она обнаружила, что никакие блоки больше не будут балансировать на вершине блока треугольной формы. Она взглянула на своего отца и показала ему блок, который ей не удалось преодолеть, чтобы оставаться на вершине, по сути говоря ему жестом: «Папа, мне нужна помощь, чтобы разобраться в этом». Ее отец показал ей, что, если она снимет треугольный блок и вместо него возьмет квадратный, она сможет сложить еще больше.Затем она добавила еще два блока к своей башне, прежде чем с гордостью показать свое творение отцу: «Дада, Оок! Оу! »
В этом обычном взаимодействии вы можете увидеть, как все области разработки Trina работают вместе. Ее физические способности позволяют ей манипулировать блоками и использовать свои мыслительные способности для выполнения своего плана по постройке башни. Она использует свой язык и социальные навыки, когда просит помощи у отца. Ее эффективное общение позволяет отцу реагировать и оказывать необходимую помощь (дальнейшее развитие ее социальных навыков, поскольку она считает себя важным и хорошим коммуникатором).Это еще больше укрепляет ее мыслительные способности, поскольку она узнает, как решить проблему увеличения высоты башни.
Что вы можете сделать
Приведенные ниже советы показывают, как вы можете помочь своему ребенку освоить математические навыки в раннем возрасте, опираясь на его природное любопытство и весело проводя время вместе. (Примечание: большинство этих советов предназначены для детей старшего возраста — в возрасте от 2 до 3 лет. Дети младшего возраста могут быть представлены рассказам и песням, используя повторение, рифмы и числа.)
Поднимайся.
Играть с сортировщиками формы. Поговорите с ребенком о каждой форме — посчитайте стороны, опишите цвета. Создавайте свои собственные фигуры, вырезая большие фигуры из цветной плотной бумаги. Попросите ребенка «прыгнуть по кругу» или «запрыгнуть на красную фигуру».
Подсчитайте и отсортируйте.
Соберите корзину с маленькими игрушками, ракушками, камешками или пуговицами. Считайте их вместе с ребенком. Отсортируйте их по размеру, цвету или назначению (то есть все машины в одной стопке, все животные в другой).
Сделайте звонок.
Вместе со своей 3-летней дочкой начните учить ее адрес и номер телефона своего дома. Поговорите с ребенком о том, что у каждого дома есть номер, и как его дом или квартира входят в серию, каждая со своим номером.
Какой это размер?
Обратите внимание на размеры объектов в мире вокруг вас: этот розовый бумажник самый большой. Синий кошелек самый маленький. Попросите ребенка подумать о своем размере по сравнению с другими предметами («Вы помещаетесь под столом? Под стулом?»).
Теперь ты готовишь!
Наполнять, перемешивать и наливать могут даже маленькие дети. Благодаря этим упражнениям дети естественным образом учатся считать, измерять, складывать и оценивать.
Уходи прочь.
Прогулка дает детям множество возможностей сравнить (какой камень больше?), Оценить (сколько желудей мы нашли?), Отметить сходства и различия (есть ли у утки мех, как у кролика?) И распределить по категориям (посмотреть, есть ли у утки мех, как у кролика?) можно найти красные листья). Вы также можете поговорить о размере (делая большие и маленькие шаги), оценить расстояние (парк рядом с нашим домом или далеко?) И потренироваться в счете (давайте посчитаем, сколько шагов мы дойдем до угла).
Время картинки.
Используйте песочные часы, секундомер или таймер для коротких (1–3 минут) занятий. Это помогает детям развить чувство времени и понять, что на одни дела уходит больше времени, чем на другие.
Поднимайся.
Укажите на разные формы и цвета, которые вы видите в течение дня. Во время прогулки вы можете увидеть знак в форме треугольника желтого цвета. Внутри магазина вы можете увидеть красный прямоугольник.
Прочтите и пой свои числа.
Пойте рифмующиеся, повторяющиеся или содержащие числа песни.Песни закрепляют закономерности (что тоже является математическим навыком). Они также являются интересным способом попрактиковаться в языке и развить такие социальные навыки, как сотрудничество.
Начни сегодня.
Используйте календарь, чтобы говорить о дате, дне недели и погоде. Календари усиливают подсчет, последовательности и закономерности. Развивайте навыки логического мышления, говоря о холодной погоде и спрашивая ребенка: что мы надеваем, когда холодно? Это побуждает вашего ребенка находить связь между холодной погодой и теплой одеждой.
Раздать.
Попросите вашего ребенка помочь в распределении таких предметов, как закуски, или в разложении салфеток на обеденном столе. Помогите ему дать каждому ребенку по крекеру. Это помогает детям понимать индивидуальную переписку. Когда вы раздаете предметы, подчеркните концепцию числа: «Один для вас, один для меня, один для папы». Или: «Мы надеваем обувь: раз, два».
Большой на блоках.
Дайте вашему ребенку возможность поиграть с деревянными блоками, пластиковыми блокировками, пустыми коробками, пакетами из-под молока и т. Д.Сложение этих игрушек в стопку и манипулирование ими помогает детям узнать о формах и отношениях между формами (например, два треугольника образуют квадрат). Скворечники и чашки для детей младшего возраста помогают им понять взаимосвязь между объектами разного размера.
Время туннеля.
Откройте большие картонные коробки с каждого конца, чтобы превратить их в туннель. Это помогает детям понять, где находится их тело в пространстве и по отношению к другим объектам.
Длинное и короткое.
Отрежьте несколько (3-5) кусочков ленты, пряжи или бумаги разной длины. Говорите о таких идеях, как длинные и короткие. Расположите ребенка в порядке от самого длинного к самому короткому.
Учитесь на ощупь.
Вырежьте фигуры — круг, квадрат, треугольник — из прочного картона. Пусть ваш ребенок коснется фигуры открытыми, а затем закрытыми глазами.
Образец воспроизведения.
Развлекайтесь с выкройками, позволяя детям раскладывать сухие макароны, крупные бусины, разные виды сухих хлопьев или кусочки бумаги разными узорами или рисунками.Во время этого занятия внимательно следите за ребенком, чтобы не подавиться, и уберите все предметы, когда закончите.
Обучение стирке.
Сделайте работу по дому интересной. Сортируя белье, попросите ребенка сделать стопку рубашек и стопку носков. Спросите его, какая стопка больше (оценка). Вместе посчитайте, сколько рубашек. Посмотрите, сможет ли он сделать пары носков: вы можете вынуть два носка и сложить их в стопку? (Не беспокойтесь, если они не совпадают! Это упражнение больше связано с подсчетом, чем с сопоставлением.)
Детская площадка по математике.
Пока ваш ребенок играет, сравнивайте его по росту (высокий / низкий), положению (больше / меньше) или размеру (большой / маленький).
Платье для успеха в математике.
Попросите ребенка выбрать рубашку на день. Спросите: Какого цвета ваша рубашка? Да, желтый. Можете ли вы найти в своей комнате что-нибудь желтое? Когда вашему ребенку исполнится три года и больше, обратите внимание на узоры на его одежде — например, полосы, цвета, формы или изображения: я вижу узор на вашей рубашке.Есть полосы, которые идут красным, синим, красным, синим. Или, ваша рубашка покрыта пони — большой пони рядом с маленьким пони, по всей вашей рубашке!
Графические игры.
Когда вашему ребенку исполнится три года и больше, составьте таблицу, на которой он сможет наклеивать стикер каждый раз, когда идет дождь или каждый раз, когда солнечно. В конце недели вы можете вместе прикинуть, в каком столбце больше или меньше наклеек, и подсчитать, сколько, чтобы быть уверенным.
Список литературы
Боуман, Б.Т., Донован М.С. и Бернс М.С. (ред.). (2001). Стремятся учиться: обучение наших дошкольников. Вашингтон, округ Колумбия: Национальная академия наук.
Diezmann, C., & Yelland, N.J. (2000). Развитие математической грамотности в раннем детстве. В Йелланде, штат Нью-Джерси (ред.), Содействие осмысленному обучению: инновации в обучении профессионалов дошкольного образования. (стр.47–58). Вашингтон, округ Колумбия: Национальная ассоциация образования детей младшего возраста.
Фромболути, К.С. и Ринк Н. (1999, июнь). Раннее детство: где начинается обучение. Министерство образования США, Управление исследований и совершенствования образования, Национальный институт развития и образования детей младшего возраста. Получено 11 мая 2018 г. по адресу https://www2.ed.gov/pubs/EarlyMath/title.html
.Помогите вашему ребенку развить ранние математические навыки • НОЛЬ ДО ТРЕХ
Дети используют первые математические навыки в повседневных делах и занятиях.Это хорошая новость, поскольку эти навыки важны для подготовки к школе. Но ранняя математика не означает вынимать калькулятор во время игры. Еще до того, как они пойдут в школу, большинство детей развивают понимание сложения и вычитания посредством повседневного взаимодействия. Например, у Томаса две машины; Джозеф хочет один. После того, как Томас поделился одной, он видит, что у него осталась одна машина (Bowman, Donovan, & Burns, 2001, p. 201). Другие математические навыки приобретаются в ходе повседневных занятий, которыми вы делитесь со своим ребенком, например, с подсчетом шагов по мере того, как вы поднимаетесь или опускаетесь.Неформальные занятия, подобные этой, дают детям толчок к формальному обучению математике, которое начинается в школе.
Какие математические знания понадобятся вашему ребенку в начальной школе? Ранние математические концепции и навыки, которые используются в учебной программе по математике в первом классе, включают: (Bowman et al., 2001, p. 76).
Размер, форма и узоры
Умение считать вербально (сначала вперед, потом назад)
Распознавающие цифры
Определение большего и меньшего количества
Понимание однозначной корреспонденции (т.е., сопоставление наборов или знание, в какой группе их четыре, а в какой пять)
Ключевые математические навыки для школы
Более продвинутые математические навыки основаны на начальном математическом «фундаменте» — точно так же, как дом построен на прочном фундаменте. В первые годы жизни вы можете помочь своему ребенку начать развивать математические навыки в раннем возрасте, представив такие идеи, как: (Из Diezmann & Yelland, 2000 и Fromboluti & Rinck, 1999.)
Смысл числа
Это умение точно считать — первый нападающий.Затем, позже в школе, дети научатся считать в обратном порядке. Более сложный навык, связанный с чувством чисел, — это способность видеть отношения между числами, например, сложение и вычитание. Бен (2 года) увидел кексы на тарелке. Он сосчитал со своим отцом: «Один, два, три, четыре, пять, шесть… »
Представительство
Реализация математических идей с помощью слов, картинок, символов и предметов (например, блоков). Кейси (3 года) собирался на пикник. Он аккуратно разложил четыре пластмассовые тарелки и четыре пластмассовых стакана: «Так что всей семьей приехать на пикник!» В его семье было четыре члена; он смог применить эту информацию к выбранному количеству тарелок и чашек.
Пространственное чувство
Позже в школе дети будут называть это «геометрией». Но для малышей он знакомит с идеями формы, размера, пространства, положения, направления и движения. Азиз (28 месяцев) хихикал внизу слайда. «Что тут смешного?» — недоумевала его тетя. «Я поднялся, — сказал Азиз, — а потом спустился!»
Измерение
Технически это определение длины, высоты и веса объекта в таких единицах, как дюймы, футы или фунты.Измерение времени (например, в минутах) также относится к этой области навыков. Габриэлла (36 месяцев) снова и снова спрашивала свою Абуэлу: «Сделать печенье? Я сделаю это! » Ее Абуэла показала ей, как наполнить мерный стакан сахаром. «Нам нужны две чашки, Габи. Наполните его один раз и положите в миску, а затем снова наполните ».
Оценка
Это способность сделать хорошее предположение о количестве или размере чего-либо. Маленьким детям это сделать очень сложно.Вы можете помочь им, показав им значение таких слов, как больше, меньше, больше, меньше, больше чем, меньше чем. Нолан (30 месяцев) посмотрел на два рогалика: один был обычным, другой — мини-бубликом. Его отец спросил: «Какой из них ты предпочитаешь?» Нолан указал на обычный рогалик. Его отец сказал: «Ты, должно быть, голоден! Этот рогалик больше. Этот бублик меньше. Хорошо, я дам тебе большую. Скоро завтрак! »
Узоры
Узоры — это вещи, числа, формы, изображения, которые логически повторяются.Шаблоны помогают детям научиться делать прогнозы, понимать, что будет дальше, устанавливать логические связи и использовать навыки рассуждения. Ава (27 месяцев) указала на Луну: «Луна. Солнце переходит ночь-ночь. Дедушка подобрал ее: «Да, маленькая Ава. Утром выходит солнце, а луна уходит. Ночью солнце засыпает, а луна выходит играть. Но пора Аве спать, прямо как солнце.
Решение проблем
Способность продумать проблему, признать, что к ответу существует более одного пути.Это означает использование прошлых знаний и навыков логического мышления для поиска ответа. Карл (15 месяцев) посмотрел на сортировщик формы — пластиковый барабан с тремя отверстиями в верхней части. Отверстия имели форму треугольника, круга и квадрата. Карл посмотрел на массивные фигуры на полу. Он поднял треугольник. Он положил его в свой месяц, а затем ударил им об пол. Он коснулся краев пальцами. Затем он попытался засунуть его в каждую дырочку новой игрушки. Сюрприз! Он упал в отверстие треугольника! Карл потянулся к другому блоку, на этот раз круглому…
Математика: одна часть целого
Математические навыки — это лишь часть более широкой сети навыков, которые дети развивают в ранние годы, включая языковые, физические и социальные навыки.Каждая из этих областей навыков зависит от других и влияет на них.
Трина (18 месяцев) укладывала блоки. Она положила два квадратных блока один на другой, а затем треугольный. Она обнаружила, что никакие блоки больше не будут балансировать на вершине блока треугольной формы. Она взглянула на своего отца и показала ему блок, который ей не удалось преодолеть, чтобы оставаться на вершине, по сути говоря ему жестом: «Папа, мне нужна помощь, чтобы разобраться в этом». Ее отец показал ей, что, если она снимет треугольный блок и вместо него возьмет квадратный, она сможет сложить еще больше.Затем она добавила еще два блока к своей башне, прежде чем с гордостью показать свое творение отцу: «Дада, Оок! Оу! »
В этом обычном взаимодействии вы можете увидеть, как все области разработки Trina работают вместе. Ее физические способности позволяют ей манипулировать блоками и использовать свои мыслительные способности для выполнения своего плана по постройке башни. Она использует свой язык и социальные навыки, когда просит помощи у отца. Ее эффективное общение позволяет отцу реагировать и оказывать необходимую помощь (дальнейшее развитие ее социальных навыков, поскольку она считает себя важным и хорошим коммуникатором).Это еще больше укрепляет ее мыслительные способности, поскольку она узнает, как решить проблему увеличения высоты башни.
Что вы можете сделать
Приведенные ниже советы показывают, как вы можете помочь своему ребенку освоить математические навыки в раннем возрасте, опираясь на его природное любопытство и весело проводя время вместе. (Примечание: большинство этих советов предназначены для детей старшего возраста — в возрасте от 2 до 3 лет. Дети младшего возраста могут быть представлены рассказам и песням, используя повторение, рифмы и числа.)
Поднимайся.
Играть с сортировщиками формы. Поговорите с ребенком о каждой форме — посчитайте стороны, опишите цвета. Создавайте свои собственные фигуры, вырезая большие фигуры из цветной плотной бумаги. Попросите ребенка «прыгнуть по кругу» или «запрыгнуть на красную фигуру».
Подсчитайте и отсортируйте.
Соберите корзину с маленькими игрушками, ракушками, камешками или пуговицами. Считайте их вместе с ребенком. Отсортируйте их по размеру, цвету или назначению (то есть все машины в одной стопке, все животные в другой).
Сделайте звонок.
Вместе со своей 3-летней дочкой начните учить ее адрес и номер телефона своего дома. Поговорите с ребенком о том, что у каждого дома есть номер, и как его дом или квартира входят в серию, каждая со своим номером.
Какой это размер?
Обратите внимание на размеры объектов в мире вокруг вас: этот розовый бумажник самый большой. Синий кошелек самый маленький. Попросите ребенка подумать о своем размере по сравнению с другими предметами («Вы помещаетесь под столом? Под стулом?»).
Теперь ты готовишь!
Наполнять, перемешивать и наливать могут даже маленькие дети. Благодаря этим упражнениям дети естественным образом учатся считать, измерять, складывать и оценивать.
Уходи прочь.
Прогулка дает детям множество возможностей сравнить (какой камень больше?), Оценить (сколько желудей мы нашли?), Отметить сходства и различия (есть ли у утки мех, как у кролика?) И распределить по категориям (посмотреть, есть ли у утки мех, как у кролика?) можно найти красные листья). Вы также можете поговорить о размере (делая большие и маленькие шаги), оценить расстояние (парк рядом с нашим домом или далеко?) И потренироваться в счете (давайте посчитаем, сколько шагов мы дойдем до угла).
Время картинки.
Используйте песочные часы, секундомер или таймер для коротких (1–3 минут) занятий. Это помогает детям развить чувство времени и понять, что на одни дела уходит больше времени, чем на другие.
Поднимайся.
Укажите на разные формы и цвета, которые вы видите в течение дня. Во время прогулки вы можете увидеть знак в форме треугольника желтого цвета. Внутри магазина вы можете увидеть красный прямоугольник.
Прочтите и пой свои числа.
Пойте рифмующиеся, повторяющиеся или содержащие числа песни.Песни закрепляют закономерности (что тоже является математическим навыком). Они также являются интересным способом попрактиковаться в языке и развить такие социальные навыки, как сотрудничество.
Начни сегодня.
Используйте календарь, чтобы говорить о дате, дне недели и погоде. Календари усиливают подсчет, последовательности и закономерности. Развивайте навыки логического мышления, говоря о холодной погоде и спрашивая ребенка: что мы надеваем, когда холодно? Это побуждает вашего ребенка находить связь между холодной погодой и теплой одеждой.
Раздать.
Попросите вашего ребенка помочь в распределении таких предметов, как закуски, или в разложении салфеток на обеденном столе. Помогите ему дать каждому ребенку по крекеру. Это помогает детям понимать индивидуальную переписку. Когда вы раздаете предметы, подчеркните концепцию числа: «Один для вас, один для меня, один для папы». Или: «Мы надеваем обувь: раз, два».
Большой на блоках.
Дайте вашему ребенку возможность поиграть с деревянными блоками, пластиковыми блокировками, пустыми коробками, пакетами из-под молока и т. Д.Сложение этих игрушек в стопку и манипулирование ими помогает детям узнать о формах и отношениях между формами (например, два треугольника образуют квадрат). Скворечники и чашки для детей младшего возраста помогают им понять взаимосвязь между объектами разного размера.
Время туннеля.
Откройте большие картонные коробки с каждого конца, чтобы превратить их в туннель. Это помогает детям понять, где находится их тело в пространстве и по отношению к другим объектам.
Длинное и короткое.
Отрежьте несколько (3-5) кусочков ленты, пряжи или бумаги разной длины. Говорите о таких идеях, как длинные и короткие. Расположите ребенка в порядке от самого длинного к самому короткому.
Учитесь на ощупь.
Вырежьте фигуры — круг, квадрат, треугольник — из прочного картона. Пусть ваш ребенок коснется фигуры открытыми, а затем закрытыми глазами.
Образец воспроизведения.
Развлекайтесь с выкройками, позволяя детям раскладывать сухие макароны, крупные бусины, разные виды сухих хлопьев или кусочки бумаги разными узорами или рисунками.Во время этого занятия внимательно следите за ребенком, чтобы не подавиться, и уберите все предметы, когда закончите.
Обучение стирке.
Сделайте работу по дому интересной. Сортируя белье, попросите ребенка сделать стопку рубашек и стопку носков. Спросите его, какая стопка больше (оценка). Вместе посчитайте, сколько рубашек. Посмотрите, сможет ли он сделать пары носков: вы можете вынуть два носка и сложить их в стопку? (Не беспокойтесь, если они не совпадают! Это упражнение больше связано с подсчетом, чем с сопоставлением.)
Детская площадка по математике.
Пока ваш ребенок играет, сравнивайте его по росту (высокий / низкий), положению (больше / меньше) или размеру (большой / маленький).
Платье для успеха в математике.
Попросите ребенка выбрать рубашку на день. Спросите: Какого цвета ваша рубашка? Да, желтый. Можете ли вы найти в своей комнате что-нибудь желтое? Когда вашему ребенку исполнится три года и больше, обратите внимание на узоры на его одежде — например, полосы, цвета, формы или изображения: я вижу узор на вашей рубашке.Есть полосы, которые идут красным, синим, красным, синим. Или, ваша рубашка покрыта пони — большой пони рядом с маленьким пони, по всей вашей рубашке!
Графические игры.
Когда вашему ребенку исполнится три года и больше, составьте таблицу, на которой он сможет наклеивать стикер каждый раз, когда идет дождь или каждый раз, когда солнечно. В конце недели вы можете вместе прикинуть, в каком столбце больше или меньше наклеек, и подсчитать, сколько, чтобы быть уверенным.
Список литературы
Боуман, Б.Т., Донован М.С. и Бернс М.С. (ред.). (2001). Стремятся учиться: обучение наших дошкольников. Вашингтон, округ Колумбия: Национальная академия наук.
Diezmann, C., & Yelland, N.J. (2000). Развитие математической грамотности в раннем детстве. В Йелланде, штат Нью-Джерси (ред.), Содействие осмысленному обучению: инновации в обучении профессионалов дошкольного образования. (стр.47–58). Вашингтон, округ Колумбия: Национальная ассоциация образования детей младшего возраста.
Фромболути, К.С. и Ринк Н. (1999, июнь). Раннее детство: где начинается обучение. Министерство образования США, Управление исследований и совершенствования образования, Национальный институт развития и образования детей младшего возраста. Получено 11 мая 2018 г. по адресу https://www2.ed.gov/pubs/EarlyMath/title.html
.10 РАЗВИТИЕ УРОВНЯ ПРЕПОДАВАНИЯ МАТЕМАТИКИ | Сложим: помощь детям в изучении математики
Кэмпбелл, П.Ф. (1996). Расширение прав и возможностей детей и учителей в классах начальной математики городских школ. Городское образование , 30 , 449–475.
Карпентер, Т. (1988). Обучение как решение проблем. В Р. И. Чарльз и Э. А. Сильвер (ред.), Обучение и оценка решения математических задач (стр. 187–202). Рестон, Вирджиния: Национальный совет учителей математики.
Карпентер, Т.П., Феннема, Э., и Франке, М.Л. (1996). Когнитивно управляемое обучение: база знаний для реформы начального обучения математике. Журнал начальной школы , 97 , 3–20.
Карпентер, Т.П., Феннема, Э., Франке, М.Л., Эмпсон, С.Б., и Леви, Л.В. (1999). Детская математика: познавательно управляемое обучение . Портсмут, Нью-Хэмпшир: Heinemann.
Карпентер, Т.П., Феннема, Э., Петерсон, П.Л., Чанг, К.П., и Лоэф, М. (1989). Использование знаний о математическом мышлении детей в классе: экспериментальное исследование. Американский журнал исследований в области образования , 26 , 499–531.
Карпентер, Т.П., и Леви, Л. (1999, апрель). Развитие представлений об алгебраическом мышлении в начальных классах. Документ, представленный на заседании Американской ассоциации исследований в области образования, Монреаль.
Clark, C.M., & Peterson, P.L. (1986). Мыслительные процессы учителей. В M.C.Wittrock (Ed.), Справочник по исследованиям по обучению (3-е изд., Стр. 225–296).Нью-Йорк: Макмиллан.
Кобб П., Вуд Т., Якель Э. Николлс Дж., Уитли Г., Тригатти Б. и Перлвиц М. (1991). Оценка проблемно-ориентированного математического проекта для второго класса. Журнал исследований в области математического образования , 22 , 3–29.
Коэн, Д.К., и Болл, Д.Л. (1999). Инструкция, возможности и улучшение (Отчет об исследовании CPRE № RR-043). Филадельфия: Университет Пенсильвании, Консорциум исследований политики в области образования.
Коэн, Д.К., и Болл, Д.Л. (2000, апрель). Инструктивное нововведение: переосмысление истории. Документ, представленный на заседании Американской ассоциации исследований в области образования, Новый Орлеан.
Конференция Совета математических наук. (2000, сентябрь). Проект отчета по проекту «Математическое образование учителей CBMS» [On-line]. Доступно: http://www.maa.org/cbms/metdraft/index.htm. [3 января 2001 г.].
Давенпорт, Л. (в печати). Учебные планы элементарной математики как инструмент реформы математического образования: проблемы внедрения и последствия для профессионального развития.В P.Smith, A.Morse, & L.Davenport (Eds.), Обучение учителей и реализация учебной программы . Ньютон, Массачусетс: Центр развития образования, Центр развития обучения.
Эрлвангер, С., и Берлангер, М. (1983). Интерпретации знака равенства у младших школьников. В J.C.Bergeron & N.Herscovics (Eds.), Proceedings of the Fifth Annual Meeting of the North American Chapter of International Group for the Psychology of Mathematics Education (vol.1. С. 250–258). Монреаль: Монреальский университет. (Номер услуги репродукции документов ERIC ED 289 688).
Фолкнер, К.П., Леви, Л., и Карпентер, Т. (1999). Детское понимание равенства: основа алгебры. Обучение детей математике , 6, 232–236.
Феннема, Э., Карпентер, Т.П., Франке, М.Л., Леви, Л., Якобс, В., и Эмпсон, Б. (1996). Продольное исследование обучения использованию детского мышления при обучении математике. Журнал исследований в области математического образования , 27 , 403–434.
Развитие понимания математики
На этой странице
Изучение математического языка
Как и все дисциплины, математика имеет особый язык, который учащиеся должны понимать, чтобы придавать смысл и развивать свои знания. Способность интерпретировать язык в различных математических контекстах и для различных целей имеет фундаментальное значение для решения математических задач.
Ди Гизи и Флеминг (2005) описывают три типа словарного запаса, который нужен учащимся для решения словесных задач:
- математический словарь
- процедурный словарь
- описательный словарь
Каждый тип словарного запаса должен быть подробно изучен, а их использование смоделировано для учащихся.
В математике существует множество семиотических или смыслообразующих систем и грамматических моделей (Schleppegrell, 2007).
С точки зрения систем создания значений, учащиеся должны переключаться между письменным языком, устным языком, символической нотацией, а также графиками и визуальными представлениями. Они также должны ознакомиться с математическими грамматическими моделями, относящимися к технической лексике, использованию синонимичных глаголов и неявным логическим отношениям.
Стратегии развития понимания математического языка
Приведенные ниже стратегии демонстрируют, как учителя могут использовать грамотность для поддержки понимания учащимися математического языка.
Ссылки
- Adams, T. (2003). Чтение по математике: больше, чем слова. Учитель чтения, 58 (8), 219–234.
- Адамс, Т.Л., Тангата, Ф., и Кинг, К. (2005). «Взвешивайте», чтобы идти! Изучение математического языка. Преподавание математики в средней школе, 10 (9), 444–448.
- Армстронг А., Минг К. и Хелф С. (2018). Грамотность по содержательной области на уроках математики. Информационный центр: журнал образовательных стратегий, проблем и идей, 91 (2), 85–95.
- Бауэрс П.Н. и Кук Г. (2012). Морфология и общие основы понимания учащимися письменного слова. Перспективы языка и грамотности, 38 (4), 31–35.
- DiGisi, L.L., & Fleming, D. (2005). Специалисты по грамотности в классе математики! Устранение разрыва в успеваемости на государственных экзаменах по математике. Голоса из середины, 13 (1), 48–52.
- Гоф Дж. (2007). Концептуальная сложность и очевидные противоречия в языке математики. Учитель математики Австралии, 63 (2), 8–16.
- МакГрегор, М., и Стейси, К. (1997). Понимание студентами алгебраических обозначений: 11-16. Образовательные исследования по математике. 33 (1), 1–19.
- О’Халлоран, К. Л. (2000). Классный дискурс по математике: мульти-семиотический анализ. Лингвистика и образование, 10 (3), 359–388.
- Пирс, М. Э. и Фонтейн, Л. М. (2009). Обучение развитию словарного запаса по математике. Учитель чтения, 63 (3), 239–243.
- Rozzelle, J. & Scearce, C. (2009). Электроинструменты для подростковой грамотности: стратегии обучения.Блумингтон, Индиана: Дерево решений.
- Шлеппегрелл, М. Дж. (2007). Лингвистические проблемы преподавания и обучения математике: обзор исследования. Ежеквартальное чтение и письмо, 23 (2), 139–159.
- ван Вондел, С., Стинбек, Х., ван Дейк, М., и ван Герт, П. (2017). Спрашивайте, не говорите; Комплексный динамический системный подход к совершенствованию естественнонаучного образования с упором на совместное построение научного понимания. Педагогика и педагогическое образование, 63, 243–253.
- Управление по учебным программам и оценке штата Виктория (VCAA).(без даты) Обучение математике. Извлекаются из Викторианский учебный план — изучение математики
- Зевенберген, Р. (2001). Математическая грамотность в среднем классе. Обучение грамоте: средние годы, 9 (2), 21–28.
Использование грамотности для поддержки решения проблем
Язык имеет фундаментальное значение для преподавания и изучения математики. Часто учащиеся должны применять навыки грамотности, чтобы читать и интерпретировать сформулированные задачи. Однако ошибки грамотности, связанные с решением задач, могут возникнуть до того, как учащиеся попытаются применить свои математические знания.
Эти ошибки грамотности, связанные с решением проблем, включают: чтение, понимание и преобразование (Newman, 1977; Clements, 1980; Clarkson, 1983).
Важность грамотности в процессах решения математических задач была подтверждена Дойлом (2005, стр. 40), который утверждал, что «чем больше учащиеся понимают информацию, тем больше у них шансов участвовать и развивать математические навыки».
Стратегии, использующие грамотность для поддержки решения проблем
Приведенные ниже стратегии демонстрируют, как учителя могут развить у учащихся навыки грамотности для поддержки решения математических задач.
Ссылки
- Clarkson, P.C. (1983). Типы ошибок, допущенных студентами из Папуа-Новой Гвинеи. Образовательные исследования по математике, 14, 355–367.
- Клементс, М. А. (1980). Анализирует ошибки детей в письменных математических задачах. Образовательные исследования по математике, 11, 1–21.
- Дойл, К. (2005). Решение математических задач: потребность в грамотности. В Бартлетт Б., Брайер Ф. и Робак Д. Стимулирование «действия» как участников совместных исследований.Международная конференция по познанию, языку и специальному образованию, 2, (стр. 39–45). Брисбен: Университет Гриффита.
- Фанг, З., и Шлеппегрелл, М. Дж. (2010). Дисциплинарная грамотность в областях содержания: поддержка вторичного чтения посредством функционального языкового анализа. Журнал по грамотности подростков и взрослых, 53 (7), 587–597.
- Фишер Д., Фрей Н. и Хэтти Дж. (2016). Наглядное обучение грамоте, классы K-12: внедрение методов, которые лучше всего работают для ускорения обучения учащихся.Таузенд-Оукс, Калифорния: Публикации SAGE.
- Джонсон, Х. и Уотсон, П. А. (2011). Чем они занимаются: дифференцируют знания и навыки грамотности по дисциплинам содержания. Журнал по грамотности подростков и взрослых, 55 (2), 100–109. Ньюман, Н. А. (1977). Анализ ошибок школьников шестого класса при выполнении письменных математических заданий. Документ, представленный на 1-й конференции Исследовательской группы математического образования Австралии, Мельбурн.
- Стейси К. и Гровс С. (2006). Стратегии решения задач: планы уроков по развитию математического мышления.Бервик, Виктория: объективные учебные материалы.




 1 (4-ые классы)
1 (4-ые классы)

 е., сопоставление наборов или знание, в какой группе их четыре, а в какой пять)
е., сопоставление наборов или знание, в какой группе их четыре, а в какой пять)