Парадокс банаха тарского простыми словами: Парадокс Банаха — Тарского | Математика, которая мне нравится
Парадокс Банаха — Тарского | Математика, которая мне нравится
Знаете ли вы, что можно разрезать шар на пять частей, из которых складывают, не растягивая их, два шара того же радиуса, что и исходный?
Эта теорема известна как парадокс Банаха — Тарского.
Так почему же мы не можем сделать это в реальной жизни, скажем, с шаром из золота? Проблема в том, что сделать это можно только с материалом, который делúм до бесконечности, чего нет в действительности. Необходимые части настолько экзотические, что у них нет меры, или объема. Парадокс Банаха — Тарского говорит о том, что как бы мы ни определяли объем, всегда найдутся множества, которые не имеют объема (неизмеримые множества), или же приведенный выше пример покажет, что .
Теорему Банаха — Тарского можно сформулировать иначе (сядьте, пожалуйста ). Возьмем шарик размером с горошину. Мы можем разрезать его на конечное число кусков так, что собрав эти куски, получим шар размером с Солнце.
Ясно, что такое трудно себе представить.
Если мы не будем исключать растяжение, то все становится гораздо понятнее. Так, взяв интервал , мы растянем его в два раза, потом разрежем пополам и получим два интервала такой же длины, что и исходный. Если мы не будем ограничивать число кусков, на которые разрезаем шар, то все тоже выглядит гораздо понятнее, поскольку число точек в одном шаре такое же, как и количество точек в двух шарах.
Доказательство парадокса Банаха — Тарского основано на изучении действия группы преобразований на сфере, в частности, подгруппы группы вращений . Эти подгруппы (свободные подгруппы двух образующих) позволяют строить “парадоксальные’’ множества — множества, конгруэнтные двум или более копиям самих себя при групповых преобразованиях. Доказательство также опирается на аксиому выбора. Идея доказательства связана с равносоставленностью.
Источник: http://www.math.hmc.edu/funfacts/ffiles/30001.1-3-8.shtml
Парадокс Банаха — Тарского — это… Что такое Парадокс Банаха — Тарского?
Шар можно «разбить» на куски и собрать из них два таких же шара.Парадокс Банаха — Тарского
Два подмножества евклидова пространства называются равносоставленными, если одно можно разбить на конечное число «кусков» и составить из них второе. При этом для удвоения шара достаточно пяти кусков, но четырёх недостаточно.
Более точно, два множества A и B являются равносоставленными, если их можно представить как конечное объединение непересекающихся подмножеств , так, что для каждого i подмножество Ai конгруэнтно Bi.
Верен также более сильный вариант парадокса:
Любые два ограниченных подмножества евклидова пространства с непустой внутренностью являются равносоставленными. |
Ввиду своей неправдоподобности, этот парадокс часто используется как довод против принятия аксиомы выбора, которая существенно используется при построении такого разбиения. Принятие подходящей альтернативной аксиомы позволяет доказать невозможность указанного разбиения, не оставляя места для этого парадокса.
Парадокс был открыт в 1926 году Стефаном Банахом и Альфредом Тарским. Очень похож на более ранний парадокс Хаусдорфа, и его доказательство основано на той же идее. Поэтому более правильно называть
Значение для теории меры
Разделяя шар на конечное число частей, мы интуитивно ожидаем, что, складывая эти части вместе, можно получить только сплошные фигуры, объём которых равен объёму исходного шара радиуса. Однако это справедливо только в случае, когда шар делится на части, имеющие объём. Суть парадокса заключается в том, что в трёхмерном пространстве существуют неизмеримые множества, которые не имеют объёма, если под объёмом мы понимаем то, что обладает свойством аддитивности, и предполагаем, что объёмы двух конгруэнтных множеств совпадают. Очевидно, что «куски» в таком разбиении не могут быть измеримыми (и невозможно осуществить такое разбиение какими-либо средствами на практике).
Однако это справедливо только в случае, когда шар делится на части, имеющие объём. Суть парадокса заключается в том, что в трёхмерном пространстве существуют неизмеримые множества, которые не имеют объёма, если под объёмом мы понимаем то, что обладает свойством аддитивности, и предполагаем, что объёмы двух конгруэнтных множеств совпадают. Очевидно, что «куски» в таком разбиении не могут быть измеримыми (и невозможно осуществить такое разбиение какими-либо средствами на практике).
Для плоского круга аналогичная теорема неверна. Более того, Банах показал, что на плоскости понятие площади может быть продолжено на все ограниченные множества как конечно-аддитивная мера, инвариантная относительно движений; в частности, любое множество, равносоставленное кругу, имеет ту же площадь. Хаусдорф показал, что подобное сделать нельзя на двумерной сфере, и, следовательно, в трёхмерном пространстве, и парадокс Банаха — Тарского даёт этому наглядную иллюстрацию.
Тем не менее, некоторые парадоксальные разбиения возможны и на плоскости: круг можно разбить на конечное число (хватает 10 Квадратура круга Тарского (англ.)).
Квадратура круга Тарского (англ.)).
Ссылки
- ↑ Miklos Laczkovich: «Equidecomposability and discrepancy: a solution to Tarski’s circle squaring problem», Crelle’s Journal of Reine and Angewandte Mathematik 404 (1990) pp. 77-117.
- ↑ Miklos Laczkovich: «Paradoxical decompositions: a survey of recent results.» First European Congress of Mathematics, Vol. II (Paris, 1992), pp. 159-184, Progr. Math., 120, Birkh.user, Basel, 1994.
Литература
Парадокс Банаха-Тарского — это… Что такое Парадокс Банаха-Тарского?
Шар можно «разбить» на куски и собрать из них два таких же шара.
Парадокс Банаха — Тарского, или парадокс удвоения шара, говорит, что трёхмерный шар равносоставлен двум своим копиям.
Два подмножества евклидова пространства называются равносоставленными, если одно можно разбить на конечное число «кусков» и составить из них второе. При этом для удвоения шара достаточно пяти кусков, но четырёх недостаточно.
Более точно, два множества A и B являются равносоставленными, если их можно представить как конечное объединение непересекающихся подмножеств , так, что для каждого
Верен также более сильный вариант парадокса:
| Любые два ограниченных подмножества евклидова пространства с непустой внутренностью являются равносоставленными. |
Ввиду своей неправдоподобности, этот парадокс часто используется как довод против принятия аксиомы выбора, которая существенно используется при построении такого разбиения. Принятие подходящей альтернативной аксиомы позволяет доказать невозможность указанного разбиения, не оставляя места для этого парадокса.
Парадокс был открыт в 1926 году Стефаном Банахом и Альфредом Тарским. Очень похож на более ранний парадокс Хаусдорфа, и его доказательство основано на той же идее. Поэтому более правильно называть

Значение для теории меры
Разделяя шар на конечное число частей, мы интуитивно ожидаем, что, складывая эти части вместе, можно получить только сплошные фигуры, объём которых равен объёму исходного шара радиуса. Однако это справедливо только в случае, когда шар делится на части, имеющие объём. Суть парадокса заключается в том, что в трёхмерном пространстве существуют неизмеримые множества, которые не имеют объёма, если под объёмом мы понимаем то, что обладает свойством аддитивности, и предполагаем, что объёмы двух конгруэнтных множеств совпадают. Очевидно, что «куски» в таком разбиении не могут быть измеримыми (и невозможно осуществить такое разбиение какими-либо средствами на практике).
Для плоского круга аналогичная теорема неверна. Более того, Банах показал, что на плоскости понятие площади может быть продолжено на все ограниченные множества как конечно-аддитивная мера, инвариантная относительно движений; в частности, любое множество, равносоставленное кругу, имеет ту же площадь. Хаусдорф показал, что подобное сделать нельзя на двумерной сфере, и, следовательно, в трёхмерном пространстве, и парадокс Банаха — Тарского даёт этому наглядную иллюстрацию.
Хаусдорф показал, что подобное сделать нельзя на двумерной сфере, и, следовательно, в трёхмерном пространстве, и парадокс Банаха — Тарского даёт этому наглядную иллюстрацию.
Тем не менее, некоторые парадоксальные разбиения возможны и на плоскости: круг можно разбить на конечное число кусков и составить из них квадрат равной площади.
Литература
Wikimedia Foundation. 2010.
Парадокс Банаха—Тарского — это… Что такое Парадокс Банаха—Тарского?
Шар можно «разбить» на куски и собрать из них два таких же шара.
Парадокс Банаха — Тарского, или парадокс удвоения шара, говорит, что трёхмерный шар равносоставлен двум своим копиям.
Два подмножества евклидова пространства называются равносоставленными, если одно можно разбить на конечное число «кусков» и составить из них второе. При этом для удвоения шара достаточно пяти кусков, но четырёх недостаточно.
Более точно, два множества A и B являются равносоставленными, если их можно представить как конечное объединение непересекающихся подмножеств , так, что для каждого i подмножество Ai конгруэнтно Bi.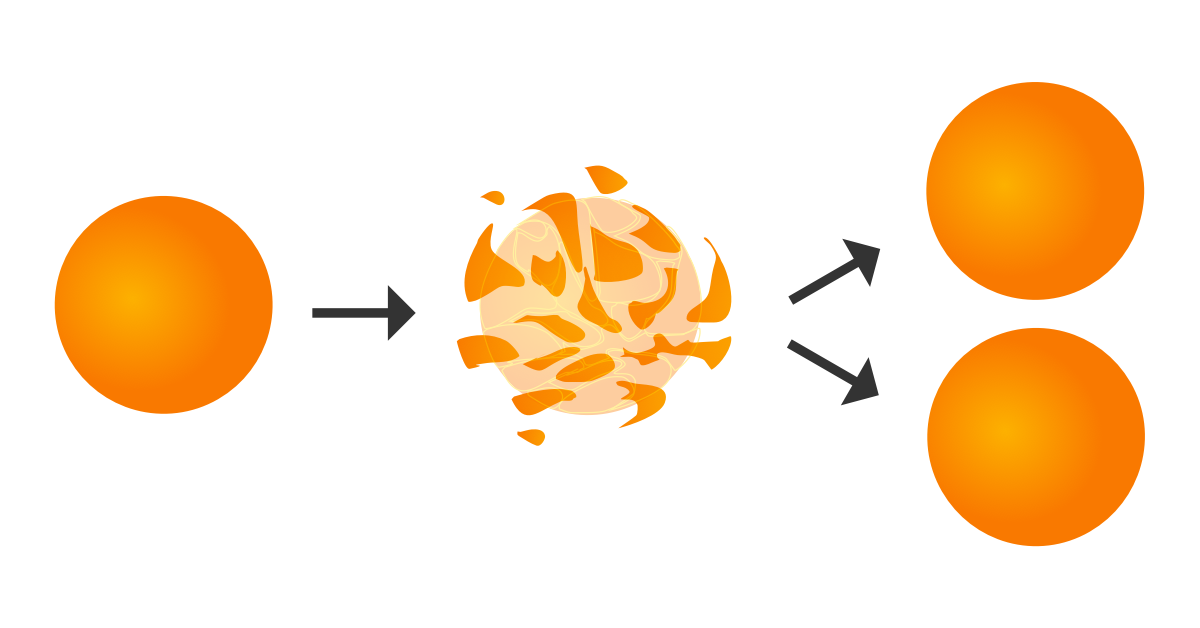
Верен также более сильный вариант парадокса:
| Любые два ограниченных подмножества евклидова пространства с непустой внутренностью являются равносоставленными. |
Ввиду своей неправдоподобности, этот парадокс часто используется как довод против принятия аксиомы выбора, которая существенно используется при построении такого разбиения. Принятие подходящей альтернативной аксиомы позволяет доказать невозможность указанного разбиения, не оставляя места для этого парадокса.
Парадокс был открыт в 1926 году Стефаном Банахом и Альфредом Тарским. Очень похож на более ранний парадокс Хаусдорфа, и его доказательство основано на той же идее. Поэтому более правильно называть парадоксом Хаусдорфа — Банаха — Тарского.
Значение для теории меры
Разделяя шар на конечное число частей, мы интуитивно ожидаем, что, складывая эти части вместе, можно получить только сплошные фигуры, объём которых равен объёму исходного шара радиуса. Однако это справедливо только в случае, когда шар делится на части, имеющие объём. Суть парадокса заключается в том, что в трёхмерном пространстве существуют неизмеримые множества, которые не имеют объёма, если под объёмом мы понимаем то, что обладает свойством аддитивности, и предполагаем, что объёмы двух конгруэнтных множеств совпадают. Очевидно, что «куски» в таком разбиении не могут быть измеримыми (и невозможно осуществить такое разбиение какими-либо средствами на практике).
Однако это справедливо только в случае, когда шар делится на части, имеющие объём. Суть парадокса заключается в том, что в трёхмерном пространстве существуют неизмеримые множества, которые не имеют объёма, если под объёмом мы понимаем то, что обладает свойством аддитивности, и предполагаем, что объёмы двух конгруэнтных множеств совпадают. Очевидно, что «куски» в таком разбиении не могут быть измеримыми (и невозможно осуществить такое разбиение какими-либо средствами на практике).
Для плоского круга аналогичная теорема неверна. Более того, Банах показал, что на плоскости понятие площади может быть продолжено на все ограниченные множества как конечно-аддитивная мера, инвариантная относительно движений; в частности, любое множество, равносоставленное кругу, имеет ту же площадь. Хаусдорф показал, что подобное сделать нельзя на двумерной сфере, и, следовательно, в трёхмерном пространстве, и парадокс Банаха — Тарского даёт этому наглядную иллюстрацию.
Тем не менее, некоторые парадоксальные разбиения возможны и на плоскости: круг можно разбить на конечное число кусков и составить из них квадрат равной площади.
Литература
Wikimedia Foundation. 2010.
Парадоксы теории множеств и их философская интерпретация / Хабр
Краткий синопсис
По образованию я физик-теоретик, однако имею неплохую математическую базу. В магистратуре одним из предметов была философия, необходимо было выбрать тему и сдать по ней работу. Поскольку большинство вариантов не единожды было обмусолено, то решил выбрать что-то более экзотическое. На новизну не претендую, просто получилось аккумулировать всю/почти всю доступную литературу по этой теме. Философы и математики могут кидаться в меня камнями, буду лишь благодарен за конструктивную критику.
P.S. Весьма «сухой язык», но вполне читабельно после университетской программы. По большей части определения парадоксов брались из Википедии (упрощённая формулировка и готовая TeX-разметка).
Введение
Как сама теория множеств, так и парадоксы, ей присущие, появились не так уж и давно, чуть более ста лет назад.
 Однако за этот период был пройден большой путь, теория множеств так или иначе фактически стала основой большинства разделов математики. Парадоксы же её, связанные с бесконечностью Кантора, были успешно объяснены буквально за половину столетия.
Однако за этот период был пройден большой путь, теория множеств так или иначе фактически стала основой большинства разделов математики. Парадоксы же её, связанные с бесконечностью Кантора, были успешно объяснены буквально за половину столетия.Следует начать с определения.
Что есть множество? Вопрос достаточно простой, ответ на него вполне интуитивен. Множество это некий набор элементов, представляемый единым объектом. Кантор в своей работе Beiträge zur Begründung der transfiniten Mengenlehre даёт определение: под «множеством» мы понимаем соединение в некое целое M определённых хорошо различимых предметов m нашего созерцания или нашего мышления (которые будут называться «элементами» множества M)[1]. Как видим, суть не изменилась, разница лишь в той части, которая зависит от мировоззрения определяющего. История же теории множеств как в логике так и в математике весьма противоречива. Фактически начало ей положил Кантор в XIX веке, далее Рассел и остальные продолжили работу.
Парадоксы (логики и теории множеств) — (греч. — неожиданный) — формально-логические противоречия, которые возникают в содержательной множеств теории и формальной логике при сохранении логической правильности рассуждения. Парадоксы возникают тогда, когда два взаимоисключающих (противоречащих) суждения оказываются в равной мере доказуемыми. Парадоксы могут появиться как в пределах научной теории, так и в обычных рассуждениях (например, приводимая Расселом перифраза его парадокса о множестве всех нормальных множеств: «Деревенский парикмахер бреет всех тех и только тех жителей своей деревни, которые не бреются сами. Должен ли он брить самого себя?»). Поскольку формально-логическое противоречие разрушает рассуждение как средство обнаружения и доказательства истины (в теории, в которой появляется парадокс, доказуемо любое, как истинное, так и ложное, предложение), возникает задача выявления источников подобных противоречий и нахождения способов их устранения. Проблема философского осмысления конкретных решений парадоксов — одна из важных методологических проблем формальной логики и логических оснований математики.
— неожиданный) — формально-логические противоречия, которые возникают в содержательной множеств теории и формальной логике при сохранении логической правильности рассуждения. Парадоксы возникают тогда, когда два взаимоисключающих (противоречащих) суждения оказываются в равной мере доказуемыми. Парадоксы могут появиться как в пределах научной теории, так и в обычных рассуждениях (например, приводимая Расселом перифраза его парадокса о множестве всех нормальных множеств: «Деревенский парикмахер бреет всех тех и только тех жителей своей деревни, которые не бреются сами. Должен ли он брить самого себя?»). Поскольку формально-логическое противоречие разрушает рассуждение как средство обнаружения и доказательства истины (в теории, в которой появляется парадокс, доказуемо любое, как истинное, так и ложное, предложение), возникает задача выявления источников подобных противоречий и нахождения способов их устранения. Проблема философского осмысления конкретных решений парадоксов — одна из важных методологических проблем формальной логики и логических оснований математики.
Целью данной работы является изучение парадоксов теории множеств как наследников античных антиномий и вполне логичных следствий перехода к новому уровню абстракции — бесконечности. Задача — рассмотреть основные парадоксы, их философскую интерпретацию.
Основные парадоксы теории множеств
Брадобрей бреет только тех людей, которые не бреются сами. Бреет ли он себя?
Продолжим кратким экскурсом в историю.
Некторые из логических парадоксов были известны с античных времён, однако по причине того, что математическая теория ограничивалась одной лишь арифметикой и геометрией, соотнести их с теорией множеств было невозможно. В XIX веке ситуация изменилась коренным образом: Кантор в своих работах вышел на новый уровень абстракции. Он ввёл понятие бесконечности, создав тем самым новый раздел математики и позволив тем самым сравнивать различные бесконечности с помощью понятия «мощность множества» [2]. Однако тем самым он породил множество парадоксов. Самым первым является так называемый парадокс Бурали-Форти. В математической литературе встречаются различные формулировки, опирающиеся на разную терминологию и предполагаемый набор известных теорем. Вот одно из формальных определений.
В математической литературе встречаются различные формулировки, опирающиеся на разную терминологию и предполагаемый набор известных теорем. Вот одно из формальных определений.
Можно доказать, что если x — произвольное множество порядковых чисел, то множество-сумма есть порядковое число, большее или равное каждому из элементов x. Предположим теперь, что — множество всех порядковых чисел. Тогда — порядковое число, большее или равное любому из чисел в . Но тогда и — порядковое число, причём уже строго большее, а значит, и не равное любому из чисел в . Но это противоречит условию, по которому — множество всех порядковых чисел.
Сущность же парадокса в том, что при образовании множества всех порядковых чисел образуется новый порядковый тип, которого ещё не было среди «всех» трансфинитных порядковых чисел, существовавших до образования множества всех порядковых чисел. Этот парадокс был обнаружен самим Кантором, независимо открыт и опубликован итальянским математиком Бурали-Форти, ошибки же последнего были исправлены Расселом, после чего формулировка приобрела окончательный вид [2,3].
Среди всех попыток избежать подобных парадоксов и в какой-то мере попробовать их объяснить наибольшего внимания заслуживает идея уже упомянутого Рассела. Он предложил исключить из математики и логики импредикативные предложения, в которых определение элемента множества зависит от последнего, что и вызывает парадоксы. Правило звучит так: «никакое множество С не может содержать элементов m, определяемых лишь в терминах множества С, а так же элементов n, предполагающих в своём определении это множество» [4]. Подобное ограничение определения множества позволяет избежать парадоксов, но при этом значительно сужает область его применения в математике. Вдобавок этого недостаточно для объяснения их природы и причин появления, коренящихся в дихотомии мышления и языка, в особенностях формальной логики [4]. В какой-то мере в данном ограничении можно проследить аналогию с тем, что в более поздний период когнитивные психологи и лингвисты начали называть «категоризацией основного уровня»: определение сведено к наиболее легкой для понимания и изучения концепцией.
Далее Кантор в 1899 году открыл парадокс, названный его именем.
Предположим, что множество всех множеств существует. В этом случае справедливо , то есть всякое множество t является подмножеством V. Но из этого следует — мощность любого множества не превосходит мощности V. Но в силу аксиомы множества всех подмножеств, для V, как и любого множества, существует множество всех подмножеств , и по теореме Кантора , что противоречит предыдущему утверждению. Следовательно, V не может существовать, что вступает в противоречие с «наивной» гипотезой о том, что любое синтаксически корректное логическое условие определяет множество, то есть что для любой формулы A, не содержащей y свободно. Замечательное доказательство отсутствия подобных противоречий на основе аксиоматизированной теории множеств Цермело-Френкеля приводится у Поттера [3].
Оба вышеуказанных парадокса с логической точки зрения идентичны «Лжецу» либо «Брадобрею»: высказываемое суждение обращено не только на нечто объективное по отношению к нему, но и само на себя. Однако следует обращать внимание не только на логическую сторону, но и на понятие бесконечности, которое тут наличествует. В литературе ссылаются на работу Пуанкаре, в которой он пишет: «вера в существование актуальной бесконечности… делает необходимым эти непредикативные определения» [2].
Однако следует обращать внимание не только на логическую сторону, но и на понятие бесконечности, которое тут наличествует. В литературе ссылаются на работу Пуанкаре, в которой он пишет: «вера в существование актуальной бесконечности… делает необходимым эти непредикативные определения» [2].
В целом же имеют место основные моменты [2]:
- в данных парадоксах нарушается правило чётко разделять „сферы“ предиката и субъекта; степень смешения близка к подмене одного понятия другим;
- обычно в логике предполагается, что в процессе рассуждения субъект и предикат сохраняют свой объём и содержание, в данном же случае происходит
переход из одной категории в другую, что даёт в результате несоответствие; - наличие слова „все“ имеет смысл для конечного числа элементов, в случае же бесконечного их количества возможно наличие такого, которое
для определения себя потребует определение множества; - нарушаются основные логические законы:
- закон тождества нарушается тогда, когда обнаруживается нетождественность себе субъекта и предиката;
- закон противоречия — когда с одинаковым правом выводятся два противоречащих друг другу суждения;
- закон исключённого третьего — когда это третье приходится признавать, а не исключать, поскольку ни первое, ни второе не могут быть признаны одно без другого, т.
 к. они оказываются одинаково правомерными.
к. они оказываются одинаково правомерными.
Третий парадокс носит имя Рассела. Один из вариантов определения приведён далее.
Пусть K — множество всех множеств, которые не содержат себя в качестве своего элемента.Содержит ли K само себя в качестве элемента? Если да, то, по определению K, оно не должно быть элементом K — противоречие.Если нет — то, по определению K, оно должно быть элементом K — вновь противоречие. Данное утверждение логически выводится из парадокса Кантора, что показывает их взаимосвязь. Однако философская сущность проявляется более чётко, поскольку „самодвижение» понятий происходит прямо “на наших глазах» [2].
Парадокс Тристрама Шенди:
В романе Стерна «Жизнь и мнения Тристрама Шенди, джентльмена» герой обнаруживает, что ему потребовался целый год, чтобы изложить события первого дня его жизни, и еще один год понадобился, чтобы описать второй день. В связи с этим герой сетует, что материал его биографии будет накапливаться быстрее, чем он сможет его обработать, и он никогда не сможет ее завершить. «Теперь я утверждаю, — возражает на это Рассел, — что если бы он жил вечно и его работа не стала бы ему в тягость, даже если бы его жизнь продолжала быть столь же богатой событиями, как вначале, то ни одна из частей его биографии не осталась бы ненаписанной».
«Теперь я утверждаю, — возражает на это Рассел, — что если бы он жил вечно и его работа не стала бы ему в тягость, даже если бы его жизнь продолжала быть столь же богатой событиями, как вначале, то ни одна из частей его биографии не осталась бы ненаписанной».
Действительно, события n-го дня Шенди мог бы описать за n-й год и, таким образом, в его автобиографии каждый день оказался бы запечатленным.
Иначе говоря, если бы жизнь длилась бесконечно, то она насчитывала бы столько же лет, сколько дней.
Рассел проводит аналогию между этим романом и Зеноном с его черепахой. По его мнению решение лежит в том, что целое эквивалентно его части в бесконечности. Т.е. к противоречию приводит только «аксиома здравого смысла» [2]. Однако же разрешение проблемы лежит в области чистой математики. Очевидно, что имеется два множества — года и дни, между элементами которых установлено взаимно-однозначное соответствие — биекция. Тогда при условии бесконечной жизни главного героя имеется два бесконечных равномощных множества, что, если рассматривать мощность как обобщение понятия количества элементов в множестве, разрешает парадокс.
Парадокс (теорема) Банаха-Тарского или парадокс удвоения шара — теорема в теории множеств, утверждающая, что трёхмерный шар равносоставлен двум своим копиям.
Два подмножества евклидова пространства называются равносоставленными, если одно можно разбить на конечное число частей, передвинуть их, и составить из них второе.
Более точно, два множества A и B являются равносоставленными, если их можно представить как конечное объединение непересекающихся подмножеств так, что для каждого i подмножество конгруэнтно .
Если же пользоваться теоремой выбора, то определение звучит так[3]:
Аксиома выбора подразумевает, что существует разбиение поверхности единичной сферы на конечное количество частей, которые преобразованиями трёхмерного Евклидова пространства, не меняющими форму этих составляющих, могут быть собраны в две сферы единичного радиуса.
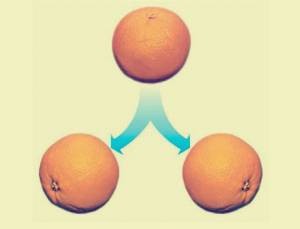
Очевидно, что при требовании для данных частей быть измеримыми, данное постоение неосуществимо. Известный физик Ричард Фейнман в своей биографии рассказывал, как в своё время у него получилось победить в споре о разбиении апельсина на конечное количество частей и пересоставлении его [5].
В определённых моментах этот парадокс используется для опровержения аксиомы выбора, однако проблема в том, что то, что мы считаем элементарной геометрией, — несущественно. Те понятия, которые мы считаем интуитивными, должны быть расширены до уровня свойств трансцендентных функций [3].
Чтобы и дальше ослабить уверенность тех, кто считает аксиому выбора неверной, следует упомянуть теорему Мазуркевича и Серпинского, которая утверждает, что существует непустое подмножество Е Евклидовой плоскости, которое имеет два непересекающихся подмножества, каждое из которых может быть разбито на конечное количество частей, так что их можно перевести изометриями в покрытие множества Е.
При этом доказательство не требует использования аксиомы выбора[3].
Дальнейшие же построения на основе аксиомы определённости дают разрешение парадокса Банаха-Тарского, но не представляют такого интереса [3].
- Парадокс Ришара: требуется назвать «наименьшее число, не названное в этой книге».
 Противоречие в том, что с одной стороны, это можно сделать, так как есть наименьшее число, названное в этой книге. Исходя из него, можно назвать и наименьшее неназванное. Но тут возникает проблема: континуум является несчётным, между двумя любыми числами можно вставить ещё бесконечное множество промежуточных чисел. С другой стороны, если бы мы могли назвать это число, оно автоматически бы перешло из класса неупомянутых в книге, в класс упомянутых [2].
Противоречие в том, что с одной стороны, это можно сделать, так как есть наименьшее число, названное в этой книге. Исходя из него, можно назвать и наименьшее неназванное. Но тут возникает проблема: континуум является несчётным, между двумя любыми числами можно вставить ещё бесконечное множество промежуточных чисел. С другой стороны, если бы мы могли назвать это число, оно автоматически бы перешло из класса неупомянутых в книге, в класс упомянутых [2]. - Парадокс Греллинга-Нильсона: слова либо знаки могут обозначать какое-либо свойство и при этом иметь его или нет. Самая тривиальная формулировка звучит так: является ли слово «гетерологичный» (что означает «неприменимый к самому себе»), гетерологичным?.. Весьма схож с парадоксом Рассела в связи с наличием диалектического противоречия: нарушается двойственность формы и содержания. В случае со словами, имеющими высокий уровень абстракции, невозможно решить, являются ли эти слова гетерологичными [2].
- Парадокс Сколема: используя теорему Гёделя о полноте и теорему Лёвенхейма-Сколема[3] получаем, что аксиоматическая теория множеств остаётся истинной и тогда, когда будет предполагаться (иметься) для её интерпретации только счётная совокупность множеств.
 В то же время
В то же время
аксиоматическая теория включает в себя уже упомянутую теорему Кантора, что приводит нас к несчётным бесконечным множествам. [2]
Разрешение парадоксов
Создание теории множеств породило то, что считают третьим кризисом математики, который до сих пор не был разрешён удовлетворительно для всех [4].
Исторически сложилось, что первым подходом был теоретико-множественный. Он основывался на использовании актуальной бесконечности, когда считалось, что любая бесконечная последовательность является завершённой в бесконечности. Идея заключалась в том, что в теории множеств часто приходилось оперировать множествами, которые могли являться части других, более обширных множеств. Успешные действия в таком случае были возможны лишь в одном случае: данные множества (конечные и бесконечные) завершены. Определённый успех был очевиден: аксиоматическая теория множеств Цермело-Френкеля, целая школа математики Николя Бурбаки, которая существует уже больше половины столетия и до сих пор вызывает множество критики.

Логицизм был попыткой свести всю известную математику к терминам арифметики, а потом термины арифметики свести к понятиям математической логики. Вплотную этим занялся Фреге, однако после окончания работы над трудом, он вынужден был указать о своей несостоятельности, после того, как Рассел указал на имеющиеся в теории противоречия. Тот же Рассел, как уже был упомянуто ранее, попытался исключить использование импредикативных определений с помощью «теории типов». Однако его понятия множества и бесконечности, а так же аксиома сводимости оказались нелогичными. Основной проблемой было то, что не учитывались качественные различия между формальной и математической логикой, а так же наличие лишних понятий, в том числе и интуитивного характера.
В итоге теория логицизма не смогла устранить диалектических противоречий парадоксов, связанных с бесконечностью. Имели место лишь принципы и методы, которые позволяли избавиться хотя бы от непредикативных определений. В свох же рассуждениях Рассел был наследником Кантора [2]
В конце XIX — начале XX в. распространение формалистической точки зрения на математику было связано с развитием аксиоматического метода и той программой обоснования математики, которую выдвинул Д. Гильберт. На степень важности этого факта указывает то, что первой проблемой из двадцати трёх, которые он поставил перед математическим сообществом, была проблема бесконечности. Формализация была необходима для доказательства непротиворечивости классической математики, «исключив при этом из неё всю метафизику». Учитывая средства и методы, которыми пользовался Гильберт, его цель оказалась принципиально невыполнимой, но его программа имела огромное влияние на все последующее развитие оснований математики. Гильберт достаточно долго работал над этой проблемой, построив первоначально аксиоматику геометрии. Поскольку решение проблемы оказалось достаточно успешным, он решил применить аксиоматический метод к теории натуральных чисел. Вот что он писал в связи с этим: «Я преследую важную цель: именно я хотел бы разделаться с вопросами обоснования математики как таковыми, превратив каждое математическое высказывание в строго выводимую формулу.
распространение формалистической точки зрения на математику было связано с развитием аксиоматического метода и той программой обоснования математики, которую выдвинул Д. Гильберт. На степень важности этого факта указывает то, что первой проблемой из двадцати трёх, которые он поставил перед математическим сообществом, была проблема бесконечности. Формализация была необходима для доказательства непротиворечивости классической математики, «исключив при этом из неё всю метафизику». Учитывая средства и методы, которыми пользовался Гильберт, его цель оказалась принципиально невыполнимой, но его программа имела огромное влияние на все последующее развитие оснований математики. Гильберт достаточно долго работал над этой проблемой, построив первоначально аксиоматику геометрии. Поскольку решение проблемы оказалось достаточно успешным, он решил применить аксиоматический метод к теории натуральных чисел. Вот что он писал в связи с этим: «Я преследую важную цель: именно я хотел бы разделаться с вопросами обоснования математики как таковыми, превратив каждое математическое высказывание в строго выводимую формулу. » От бесконечности при этом планировалось избавиться с помощью сведения её к некому конечному числу операций. Для этого он обращался к физике с её атомизмом, дабы показать всю несостоятельность бесконечных величин. Фактически Гильберт поставил вопрос о соотношении теории и объективной реальности.
» От бесконечности при этом планировалось избавиться с помощью сведения её к некому конечному числу операций. Для этого он обращался к физике с её атомизмом, дабы показать всю несостоятельность бесконечных величин. Фактически Гильберт поставил вопрос о соотношении теории и объективной реальности.
Более или менее полное представление о финитных методах дает ученик Гильберта Ж. Эрбран. Под финитными рассуждениями он понимает такие рассуждения, которые удовлетворяют следующим условиям: логические парадоксы » — всегда рассматривается лишь конечное и определенное число предметов и функций;
— функции имеют точное определение, и это определение позволяет нам вычислить их значение;
— никогда не утверждается «Этот объект существует», если не известен способ его построения;
— никогда не рассматривается множество всех предметов X какой-либо бесконечной совокупности;
— если известно, что какое-либо рассуждение или теорема верны для всех этих X, то это означает, что это общее рассуждение можно повторить для каждого конкретного X, причем само это общее рассуждение следует рассматривать только как образец для проведения таких конкретных рассуждений. «
«
Однако в момент последней публикации в этой области Гёдель уже получил свои результаты, в сущности опять обнаружил и утвердил наличие диалектики в процессе познания. По сути своей дальнейшее развитие математики продемонстрировало несостоятельность программы Гильберта.
Что же, собственно, доказал Гёдель? Можно выделить три основных результата:
1. Гёдель показал невозможность математического доказательства непротиворечивости любой системы, достаточно обширной, чтобы включать в себя всю арифметику, доказательства, которое не использовало бы каких-либо иных правил вывода, кроме тех, что имеются в самой данной системе. Такое доказательство, которое использует более мощное правило вывода, может оказаться полезным. Но если эти правила вывода сильнее логических средств арифметического исчисления, то уверенности в непротиворечивости используемых в доказательстве допущений не будет. Во всяком случае, если используемые методы не будут финитистскими, то программа Гильберта окажется невыполнимой. Гёдель как раз и показывает несостоятельность расчетов на нахождение финитистского доказательства непротиворечивости арифметики.
Гёдель как раз и показывает несостоятельность расчетов на нахождение финитистского доказательства непротиворечивости арифметики.
2. Гёдель указал на принципиальную ограниченность возможностей аксиоматического метода: система Principia Mathematica, как и всякая иная система, с помощью которой строится арифметика, существенно неполна, т. е. для любой непротиворечивой системы арифметических аксиом имеются истинные арифметические предложения, которые не выводятся из аксиом этой системы.
3. Теорема Гёделя показывает, что никакое расширение арифметической системы не может сделать ее полной, и даже если мы наполним ее бесконечным множеством аксиом, то в новой системе всегда найдутся истинные, но не выводимые средствами этой системы положения. Аксиоматический подход к арифметике натуральных чисел не в состоянии охватить всю область истинных арифметических суждений, и то, что мы понимаем под процессом математического доказательства, не сводится к использованию аксиоматического метода. После теоремы Гёделя стало бессмысленно рассчитывать, что понятию убедительного математического доказательства можно будет придать раз и навсегда очерченные формы. [2,4,6]
После теоремы Гёделя стало бессмысленно рассчитывать, что понятию убедительного математического доказательства можно будет придать раз и навсегда очерченные формы. [2,4,6]
Последним в этой череде попыток объяснить теорию множеств был интуиционизм.
Он прошел ряд этапов в своей эволюции — полуинтуиционизм, собственно интуиционизм, ультраинтуиционизм. На разных этапах математиков волновали разные проблемы, но одной из основных проблем математики является проблема бесконечности. Математические понятия бесконечности, непрерывности служили предметом философского анализа с момента их появления (идеи атомистов, апории Зенона Элейского, инфинитезимальные методы в античности, исчисление бесконечно малых в Новое время и пр.). Наибольшие споры вызывало применение различных видов бесконечности (потенциальной, актуальной) как математических объектов и их интерпретация. Все эти проблемы, на наш взгляд, были порождены более глубокой проблемой — о роли субъекта в научном познании. Дело в том, что состояние кризиса в математике порождено эпистемологической неопределенностью соизмерения мира объекта (бесконечности) и мира субъекта. Математик как субъект имеет возможность выбора средств познания — или потенциальной, или актуальной бесконечности. Применение потенциальной бесконечности как становящейся, дает ему возможность осуществлять, конструировать бесконечное множество построений, которые можно надстраивать над конечными, не имея конечного шага, не завершая построение, оно только возможно. Применение актуальной бесконечности дает ему возможность работать с бесконечностью как с уже осуществимой, завершенной в своем построении, как актуально данной одновременно.
Математик как субъект имеет возможность выбора средств познания — или потенциальной, или актуальной бесконечности. Применение потенциальной бесконечности как становящейся, дает ему возможность осуществлять, конструировать бесконечное множество построений, которые можно надстраивать над конечными, не имея конечного шага, не завершая построение, оно только возможно. Применение актуальной бесконечности дает ему возможность работать с бесконечностью как с уже осуществимой, завершенной в своем построении, как актуально данной одновременно.
На этапе полуинтуиционизма проблема бесконечности еще не была самостоятельной, а была вплетена в проблему построения математических объектов и способов его обоснования. Полуинтуиционизм А. Пуанкаре и представителей парижской школы теории функций Бэра, Лебега и Бореля был направлен против принятия аксиомы свободного выбора, с помощью которой доказывается теорема Цермело, утверждавшая, что всякое множество можно сделать вполне упорядоченным, но без указания теоретического способа определения элементов любого подмножества искомого множества. Нет способа построения математического объекта, нет и самого математического объекта. Математики считали, что наличие или отсутствие теоретического способа построения последовательности объектов исследования может служить основой обоснования или опровержения этой аксиомы. В российском варианте полуинтуиционистская концепция в философских основаниях математики получила развитие в таком направлении, как эффективизм, развиваемый Н.Н. Лузиным. Эффективизм представляет собой оппозицию к основным абстракциям учения множества Кантора о бесконечном — актуальности, выбора, трансфинитной индукции и др.
Нет способа построения математического объекта, нет и самого математического объекта. Математики считали, что наличие или отсутствие теоретического способа построения последовательности объектов исследования может служить основой обоснования или опровержения этой аксиомы. В российском варианте полуинтуиционистская концепция в философских основаниях математики получила развитие в таком направлении, как эффективизм, развиваемый Н.Н. Лузиным. Эффективизм представляет собой оппозицию к основным абстракциям учения множества Кантора о бесконечном — актуальности, выбора, трансфинитной индукции и др.
Для эффективизма гносеологически более ценными абстракциями является абстракция потенциальной осуществимости, чем абстракция актуальной бесконечности. Благодаря этому становится возможным введение понятия о трансфинитных ординалах (бесконечных порядковых числах) на основе эффективного понятия о росте функций. Гносеологическая установка эффективизма для отображения непрерывного (континуума) опиралась на дискретные средства (арифметики) и созданную Н. Н.Лузиным дескриптивную теорию множеств (функций). Интуиционизм голландца Л. Э. Я. Брауэра, Г. Вейля, А. Гейтинга в качестве традиционного объекта исследования видит свободно становящиеся последовательности различных видов. На этом этапе, решая собственно математические проблемы, в том числе о перестройке всей математики на новой основе, интуиционисты подняли философский вопрос о роли математика как познающего субъекта. Каково его положение, где он более свободен и активен в выборе средств познания? Интуиционисты первыми (и на этапе полуинтуиционизма) стали критиковать концепцию актуальной бесконечности, канторовскую теорию множеств, усмотрев в ней ущемление возможностей субъекта влиять на процесс научного поиска решения конструктивной задачи. В случае использования потенциальной бесконечности субъект себя не обманывает, так как для него идея потенциальной бесконечности интуитивно значительно яснее, чем идея актуальной бесконечности. Для интуициониста объект считается существующим, если он дан непосредственно математику или известен метод его построения, конструирования.
Н.Лузиным дескриптивную теорию множеств (функций). Интуиционизм голландца Л. Э. Я. Брауэра, Г. Вейля, А. Гейтинга в качестве традиционного объекта исследования видит свободно становящиеся последовательности различных видов. На этом этапе, решая собственно математические проблемы, в том числе о перестройке всей математики на новой основе, интуиционисты подняли философский вопрос о роли математика как познающего субъекта. Каково его положение, где он более свободен и активен в выборе средств познания? Интуиционисты первыми (и на этапе полуинтуиционизма) стали критиковать концепцию актуальной бесконечности, канторовскую теорию множеств, усмотрев в ней ущемление возможностей субъекта влиять на процесс научного поиска решения конструктивной задачи. В случае использования потенциальной бесконечности субъект себя не обманывает, так как для него идея потенциальной бесконечности интуитивно значительно яснее, чем идея актуальной бесконечности. Для интуициониста объект считается существующим, если он дан непосредственно математику или известен метод его построения, конструирования. Субъект в любом случае может приступить к процессу достраивания ряда элементов своего множества. Непостроенный объект для интуиционистов не существует. В то же время субъект, работающий с актуальной бесконечностью, будет лишен этой возможности и будет чувствовать двойную уязвимость принятой позиции:
Субъект в любом случае может приступить к процессу достраивания ряда элементов своего множества. Непостроенный объект для интуиционистов не существует. В то же время субъект, работающий с актуальной бесконечностью, будет лишен этой возможности и будет чувствовать двойную уязвимость принятой позиции:
1) никогда нельзя осуществить это бесконечное построение;
2) он принимает решение оперировать с актуальной бесконечностью как с конечным объектом и в этом случае теряет свою специфику понятия бесконечности. Интуиционизм сознательно ограничивает возможности математика тем, что тот может осуществлять построение математических объектов исключительно посредством таких средств, которые хотя и получаемы с помощью абстрактных понятий, но эффективны, убедительны, доказуемы, функционально конструктивны именно практически и сами интуитивно ясны как конструкции, построения, надежность которых на практике не вызывает никаких сомнений. Интуиционизм, опираясь на понятие потенциальной бесконечности и конструктивные методы исследования, имеет дело с математикой становления, теория множеств относится к математике бытия.
Для интуициониста Брауэра как представителя математического эмпиризма логика вторична, он критикует ее и закон исключённого третьего.
В своих отчасти мистических работах он не отрицает наличие бесконечности, однако не допускает её актуализации, лишь потенциализацию. Главное для него — интерпретация и обоснование практически используемых логических средств и математических рассуждений. Принятое интуиционистами ограничение преодолевает неопределенность использования понятия бесконечности в математике и выражает стремление преодолеть кризис в основании математики.
Ультраинтуиционизм (А.Н. Колмогоров, А.А.Марков и др.) — последняя стадия развития интуиционизма, на которой модернизируются, существенно дополняются и преобразуются основные его идеи, не изменяя его сущности, но преодолевая недостатки и усиливая позитивные стороны, руководствуясь критериями математической строгости. Слабостью подхода интуиционистов было узкое понимание роли интуиции как единственного источника обоснования правильности и эффективности математических методов. Принимая «интуитивную ясность» в качестве критерия истинности в математике, интуиционисты методологически обедняли возможности математика как субъекта познания, сводили его деятельность лишь к мыслительным операциям на основе интуиции и не включали практику в процесс математического познания. Ультраинтуиционистская программа обоснования математики является российским приоритетом. Поэтому отечественные математики, преодолевая ограниченность интуиционизма, принимали действенной методологию материалистической диалектики, признающей человеческую практику источником формирования как математических понятий, так и математических методов (умозаключений, построений). Проблему существования математических объектов ультраинтуиционисты решали, опираясь уже не на неопределяемое субъективное понятие интуиции, а на математическую практику и конкретный механизм построения математического объекта — алгоритм, выражаемый вычислимой, рекурсивной функцией.
Принимая «интуитивную ясность» в качестве критерия истинности в математике, интуиционисты методологически обедняли возможности математика как субъекта познания, сводили его деятельность лишь к мыслительным операциям на основе интуиции и не включали практику в процесс математического познания. Ультраинтуиционистская программа обоснования математики является российским приоритетом. Поэтому отечественные математики, преодолевая ограниченность интуиционизма, принимали действенной методологию материалистической диалектики, признающей человеческую практику источником формирования как математических понятий, так и математических методов (умозаключений, построений). Проблему существования математических объектов ультраинтуиционисты решали, опираясь уже не на неопределяемое субъективное понятие интуиции, а на математическую практику и конкретный механизм построения математического объекта — алгоритм, выражаемый вычислимой, рекурсивной функцией.
Ультраинтуиционизм усиливает достоинства интуиционизма, заключающиеся в возможности упорядочивания и обобщения приемов решения конструктивных проблем, употребляемых математиками любого направления. Поэтому интуиционизм последней стадии (ультраинтуиционизм) близок конструктивизму в математике. В гносеологическом аспекте основные идеи и принципы ультраинтуиционизма таковы: критика классической аксиоматики логики; использование и значительное усиление (по явному указанию А.А. Маркова) роли абстракции отождествления (мысленного отвлечения от несходных свойств предметов и одновременного вычленения общих свойств предметов) как способа построения и конструктивного понимания абстрактных понятий, математических суждений; доказательство непротиворечивости непротиворечивых теорий. В формальном аспекте применение абстракции отождествления оправдывается тремя ее свойствами (аксиомами) равенства — рефлексивности, транзитивности и симметрии.
Поэтому интуиционизм последней стадии (ультраинтуиционизм) близок конструктивизму в математике. В гносеологическом аспекте основные идеи и принципы ультраинтуиционизма таковы: критика классической аксиоматики логики; использование и значительное усиление (по явному указанию А.А. Маркова) роли абстракции отождествления (мысленного отвлечения от несходных свойств предметов и одновременного вычленения общих свойств предметов) как способа построения и конструктивного понимания абстрактных понятий, математических суждений; доказательство непротиворечивости непротиворечивых теорий. В формальном аспекте применение абстракции отождествления оправдывается тремя ее свойствами (аксиомами) равенства — рефлексивности, транзитивности и симметрии.
Для решения основного противоречия в математике по проблеме бесконечности, породившего кризис ее оснований, на этапе ультраинтуиционизма в работах А.Н. Колмогорова были предложены пути выхода из кризиса посредством решения проблемы отношений между классической и интуиционистской логикой, классической и интуиционистской математикой. Интуиционизм Брауэра в целом отрицал логику, но так как любой математик не может обойтись без логики, в интуиционизме все-таки сохранилась практика логических рассуждений, допускались некоторые принципы классической логики, имеющей в качестве своей базы аксиоматику. С.К. Клини, Р. Весли даже отмечают, что интуиционистскую математику можно описать в виде некоторого исчисления, а исчисление является способом организации математического знания на основах логики, формализации и ее формы — алгоритмизации. Новый вариант соотношения логики и математики в рамках интуиционистских требований к интуитивной ясности суждений, особенно тех, которые включали отрицание, А.Н. Колмогоров предложил следующим образом: интуиционистскую логику, тесно связанную с интуиционистской математикой, он представил в форме аксиоматического импликативного минимального исчисления высказываний и предикатов. Тем самым ученый представил новую модель математического знания, преодолевающую ограниченность интуиционизма в признании лишь интуиции как средства познания и ограниченность логицизма, абсолютизирующего возможности логики в математике.
Интуиционизм Брауэра в целом отрицал логику, но так как любой математик не может обойтись без логики, в интуиционизме все-таки сохранилась практика логических рассуждений, допускались некоторые принципы классической логики, имеющей в качестве своей базы аксиоматику. С.К. Клини, Р. Весли даже отмечают, что интуиционистскую математику можно описать в виде некоторого исчисления, а исчисление является способом организации математического знания на основах логики, формализации и ее формы — алгоритмизации. Новый вариант соотношения логики и математики в рамках интуиционистских требований к интуитивной ясности суждений, особенно тех, которые включали отрицание, А.Н. Колмогоров предложил следующим образом: интуиционистскую логику, тесно связанную с интуиционистской математикой, он представил в форме аксиоматического импликативного минимального исчисления высказываний и предикатов. Тем самым ученый представил новую модель математического знания, преодолевающую ограниченность интуиционизма в признании лишь интуиции как средства познания и ограниченность логицизма, абсолютизирующего возможности логики в математике. Эта позиция позволила в математической форме продемонстрировать синтез интуитивного и логического как основы гибкой рациональности и ее конструктивной эффективности.
Эта позиция позволила в математической форме продемонстрировать синтез интуитивного и логического как основы гибкой рациональности и ее конструктивной эффективности.
Выводы. Таким образом, эпистемологический аспект математического познания позволяет оценить революционные изменения на этапе кризиса оснований математики на рубеже XIX-XX вв. с новых позиций в понимании процесса познания, природы и роли субъекта в нем. Гносеологический субъект традиционной теории познания, соответствующий периоду господства теоретико-множественного подхода в математике, — это абстрактный, неполный, «частичный» субъект, представленный в субъектно-объектных отношениях, оторванный абстракциями, логикой, формализмом от действительности, рационально, теоретически познающий свой объект и понимаемый как зеркало, точно отражающее и копирующее действительность. По сути, субъект исключался из познания как реального процесса и результата взаимодействия с объектом. Выход интуиционизма на арену борьбы философских направлений в математике привел к новому пониманию математика как субъекта познания — человека познающего, философская абстракция которого должна быть выстроена как бы заново. Математик предстал как эмпирический субъект, понимаемый уже как целостный реальный человек, включающий все те свойства, от которых отвлекались в гносеологическом субъекте, — эмпирическую конкретность, изменчивость, историчность; это действующий и познающий в реальном познании, творческий, интуитивный, изобретательный субъект. Философия интуиционистской математики стала базой, фундаментом современной эпистемологической парадигмы, построенной на концепции гибкой рациональности, в которой человек — это цельный (целостный) субъект познания, обладающий новыми познавательными качествами, методами, процедурами; он синтезирует свою как абстрактно-гносеологическую и логико-методологическую природу и форму, так и одновременно получает экзистенциально-антропологическое и «историко-метафизическое» осмысление.
Математик предстал как эмпирический субъект, понимаемый уже как целостный реальный человек, включающий все те свойства, от которых отвлекались в гносеологическом субъекте, — эмпирическую конкретность, изменчивость, историчность; это действующий и познающий в реальном познании, творческий, интуитивный, изобретательный субъект. Философия интуиционистской математики стала базой, фундаментом современной эпистемологической парадигмы, построенной на концепции гибкой рациональности, в которой человек — это цельный (целостный) субъект познания, обладающий новыми познавательными качествами, методами, процедурами; он синтезирует свою как абстрактно-гносеологическую и логико-методологическую природу и форму, так и одновременно получает экзистенциально-антропологическое и «историко-метафизическое» осмысление.
Важным моментом так же является интуиция в познании и, в частности, в образовании математических понятий. Опять же идёт борьба с философией, попытки исключить закон исключённого третьего, как не имеющий смысла в математике и пришедший в неё из философии. Однако же наличие излишнего акцента на интуицию и отстутствие чётких математических обоснований не позволили перевести математику на твёрдый фундамент. [2,4,7]
Однако же наличие излишнего акцента на интуицию и отстутствие чётких математических обоснований не позволили перевести математику на твёрдый фундамент. [2,4,7]
Однако после появления в 1930-х годах строгого понятия алгоритма эстафету от интуиционизма принял математический конструктивизм, представители которого внесли немалый вклад в современную теорию вычислимости. Кроме того, в 1970-е и 1980-е годы обнаружились существенные связи между некоторыми идеями интуиционистов (даже теми, которые раньше казались абсурдными) и математической теорией топосов. Математика, имеющаяся в некоторых топосах, весьма напоминает ту, которую пытались создать интуиционисты.
В качестве итога можно сделать утверждение: большинство из вышеуказанных парадоксов попросту не существуют в теории множеств с самопринадлежностью [8]. Является ли подобный подход окончательным — спорный вопрос, дальнейшие работы в этой области покажут.
Заключение
Диалектико-материалистический анализ показывает, что парадоксы являются следствием дихотомии языка и мышления, выражением глубоких диалектических (теорема Гёделя позволила проявить диалектику в процессе познания) и гносеологических трудностей, связанных с понятиями предмета и предметной области в формальной логике, множества (класса) в логике и теории множеств, с употреблением принципа абстракции, позволяющего вводить в рассмотрение новые (абстрактные) объекты (бесконечность), со способами определения абстрактных объектов в науке и т.
 п. Поэтому не может быть дано универсального способа устранения всех парадоксов.
п. Поэтому не может быть дано универсального способа устранения всех парадоксов.Закончен ли третий кризис математики (потому как он находился в причинно-следственной связи с парадоксами; теперь же парадоксы — неотъемлемая часть) — тут мнения расходятся, хотя формально известные парадоксы к 1907-му году были устранены. Впрочем, сейчас в математике имеются и другие обстоятельства, которые можно считать либо кризисными, либо предвещающими кризис (например), отсутствие строгого обснования у континуального интеграла).
Что же касается парадоксов, то весьма важную роль в математике сыграл известный парадокс лжеца, а так же целая серия парадоксов в так называемой наивной (предшествовавшей аксиоматической) теории множеств, вызвавших кризис оснований (один из таких парадоксов сыграл роковую роль в жизни Г. Фреге). Но, возможно, одним из самых недооценённых явлений в современной математике, которое вполне можно назвать и парадоксальным, и кризисным, является решение Полом Коэном в 1963 году первой проблемы Гильберта. Точнее, не сам факт решения, а характер этого решения [9].
Точнее, не сам факт решения, а характер этого решения [9].
Литература
- Georg Cantor. Beiträge zur begründung der transfiniten mengenlehre. Mathematische Annalen, 46:481—512, 1895.
- И.Н. Бурова. Парадоксы теории множеств и диалектика. Наука, 1976.
- M.D. Potter. Set theory and its philosophy: a critical introduction. Oxford University Press, Incorporated, 2004.
- Жуков Н.И. Философские основания математики. Мн.: Университетское, 1990.
- Фейнман Р.Ф., С. Ильин. Вы, конечно, шутите, мистер Фейнман!: похождения удивительного человека, поведанные им Р. Лейтону. КоЛибри, 2008.
- О. М. Мижевич. Два способа преодоления парадоксов в теории множеств Г. Кантора. Логико-философские штудии, (3):279—299, 2005.
- С. И. Масалова. ФИЛОСОФИЯ ИНТУИЦИОНИСТСКОЙ МАТЕМАТИКИ. Вестник ДГТУ, (4), 2006.
- Чечулин В.Л. Теория множеств с самопринадлежностью (основания и некоторые приложения). Перм. гос. ун-т.
 – Пермь, 2012.
– Пермь, 2012. - С. Н. Тронин. Краткий конспект лекций по дисциплине »Философия математики». Казань, 2012.
- Гришин В.Н., Бочвар Д.А. Исследования по теории множеств и неклассическим логикам. Наука, 1976.
- Хофштадтер Д. Гедель, Эшер, Бах: эта бесконечная гирлянда. Бахрах-М, 2001.
- Кабаков Ф.А., Мендельсон Э. Введение в математическую логику. Издательство «Наука», 1976.
- Д.А. Бочвар. К вопросу о парадоксах математической логики и теории множеств. Математический сборник, 57(3):369—384, 1944.
Парадокс Банаха — Тарского — Википедия
Шар можно «разбить» на куски и собрать из них два таких же шара.Парадо́кс Ба́наха — Та́рского (также называется парадо́ксом удвое́ния ша́ра и парадоксом Хаусдорфа — Ба́наха — Та́рского) — теорема в теории множеств, утверждающая, что трёхмерный шар равносоставлен двум своим копиям.
Два подмножества евклидова пространства называются равносоставленными, если одно можно разбить на конечное число (не обязательно связных) попарно непересекающихся частей, передвинуть их (при этом частям не запрещается «проходить друг сквозь друга», то есть не требуется оставаться попарно непересекающимися во всех промежуточных положениях), и составить из них второе. {n}B_{i}} так, что для каждого i{\displaystyle i} подмножество Ai{\displaystyle A_{i}} конгруэнтно Bi{\displaystyle B_{i}}.
{n}B_{i}} так, что для каждого i{\displaystyle i} подмножество Ai{\displaystyle A_{i}} конгруэнтно Bi{\displaystyle B_{i}}.
Доказано, что для удвоения шара достаточно пяти частей, но четырёх недостаточно.
Верен также более сильный вариант парадокса:
|
Ввиду того, что вывод этой теоремы может показаться неправдоподобным, она иногда используется как довод против принятия аксиомы выбора, которая существенно используется при построении такого разбиения. Принятие подходящей альтернативной аксиомы позволяет доказать невозможность указанного разбиения, не оставляя места для этого парадокса.
Удвоение шара, хотя и кажется весьма подозрительным с точки зрения повседневной интуиции (в самом деле, нельзя же из одного апельсина сделать два при помощи одного только ножа), тем не менее не является парадоксом в логическом смысле этого слова, поскольку не приводит к логическому противоречию наподобие того, как к логическому противоречию приводит так называемый парадокс брадобрея или парадокс Рассела.
История
Парадокс был открыт в 1926 году Стефаном Банахом и Альфредом Тарским. Очень похож на более ранний парадокс Хаусдорфа, и его доказательство основано на той же идее.
Значение для теории меры
Разделяя шар на конечное число частей, мы интуитивно ожидаем, что, складывая эти части вместе, можно получить только сплошные фигуры, объём которых равен объёму исходного шара.
Однако это справедливо только в случае, когда шар делится на части, имеющие объём.
Суть парадокса заключается в том, что в трёхмерном пространстве существуют неизмеримые множества, которые не имеют объёма, если под объёмом мы понимаем то, что обладает свойством аддитивности, и предполагаем, что объёмы двух конгруэнтных множеств совпадают.
Очевидно, что «куски» в таком разбиении не могут быть измеримыми (и невозможно осуществить такое разбиение какими-либо средствами на практике).
Для плоского круга аналогичное свойство неверно.
Более того, Банах показал, что на плоскости понятие площади может быть продолжено на все ограниченные множества как конечно-аддитивная мера, инвариантная относительно движений; в частности, любое множество, равносоставленное кругу, имеет ту же площадь.
Хаусдорф показал, что подобное сделать нельзя на двумерной сфере, и, следовательно, в трёхмерном пространстве, и парадокс Банаха — Тарского даёт этому наглядную иллюстрацию.
Тем не менее, некоторые парадоксальные разбиения возможны и на плоскости: круг можно разбить на конечное число частей и составить из них квадрат равной площади[1][2] (квадратура круга Тарского).
Примечания
- ↑ Miklos Laczkovich: «Equidecomposability and discrepancy: a solution to Tarski’s circle squaring problem», Crelle’s Journal of Reine and Angewandte Mathematik 404 (1990) pp. 77-117.
- ↑ Miklos Laczkovich: «Paradoxical decompositions: a survey of recent results.» First European Congress of Mathematics, Vol. II (Paris, 1992), pp. 159—184, Progr. Math., 120, Birkh.user, Basel, 1994.
Литература
Объяснение парадокса Банаха-Тарского непрофессионалам — сборник рассуждений
Парадокс Банаха – Тарского — это теорема в теоретико-множественной геометрии, которая утверждает, что твердый шар в трехмерном пространстве можно разбить на конечное число неперекрывающихся частей, которые затем можно собрать вместе другим способом, чтобы получить две одинаковых копии оригинального шара.
—Википедия
На самом деле, что касается математических тем, вики часто сбивает вас с толку еще больше, чем вы были раньше.Но этот неплохой. (Не * так * плохо.)
Парадокс Банаха-Тарского в качестве темы выбрал Патрик К., посещающий SMU. Идея парадокса заключается в том, что вы можете удвоить объем трехмерного набора точек без добавления новых точек. Почему это парадокс? Что ж, это бросает вызов интуиции, потому что в повседневной жизни мы обычно никогда не видим, как один объект волшебным образом превращается в две равные копии самого себя.
Потому что это невозможно в нашем физическом мире. Математическая версия парадокса использует концепцию неизмеримого множества .Каждый объект в реальной жизни — это измеримых , потому что это набор конечного числа атомов, занимающих конечное количество пространства. С математической точки зрения, даже когда конечное становится бесконечным, у вас все еще есть измеримые множества. Надо действительно очень постараться, чтобы создать неизмеримый набор.
Парадокс Банаха-Тарского разбивает сферу на конечное число неизмеримых множеств точек. Ключевое слово — конечное . Фактически, можно показать, что его можно разделить всего на ПЯТЬ частей, одна из которых является точкой в центре.Итак, с другими четырьмя частями мы можем разделить их на две группы по две и создать целую сферу из каждой группы, каждая такого же размера, что и исходная сфера.
Хотя это невозможно сделать в реальной жизни (потому что мы ограничены атомами), можно провести аналогию из реальной жизни. Эта аналогия потребует базовых знаний о газовых законах, а именно о том, что давление и объем обратно пропорциональны. Вот так.
Рассмотрим легко растягиваемый воздушный шар с некоторым объемом газа внутри.Теперь выпустите газ в какой-нибудь контейнер и разделите газ в контейнере, чтобы заполнить два шара. Каждый новый воздушный шар будет иметь половину объема оригинала. Но мы собираемся ввести трюк. Мы снизим наполовину давление в комнате. Это приводит к тому, что каждый воздушный шар расширяется в два раза, так что каждый из них становится такого же размера, как оригинал. Мы реконструировали парадокс!
Это приводит к тому, что каждый воздушный шар расширяется в два раза, так что каждый из них становится такого же размера, как оригинал. Мы реконструировали парадокс!
Но подождите, скажете вы! Несмотря на то, что каждый новый воздушный шар имеет тот же объем , что и оригинал, он имеет только половину плотности .Так что это не тот воздушный шарик, что и оригинал.
Это возражение верно для физического мира. Но в математике мы МОЖЕМ получить две одинаковые сферы из одной. Вот в чем загвоздка. Математическая сфера имеет бесконечную плотность. Когда вы разрезаете бесконечную плотность пополам, новая плотность по-прежнему… бесконечность. Это объясняет парадокс.
Кроме того, чтобы увидеть этот парадокс, вам понадобится вещь, называемая Аксиомой выбора. Вы можете прочитать об этом статью в вики, если хотите; тем не менее, приготовьтесь познакомиться с настоящей математикой.
Извините за опоздание с этим постом; У меня был напряженный день, в том числе я много писала. Я немного выгорел от написания к 17:00, и к тому времени, когда я начал этот пост, мне действительно не хотелось писать. Чтобы разобраться в некоторых вещах о Банахе-Тарском, я провел несколько фактических исследований, как в Интернете, так и в моем учебнике по математике, в котором были аннотации о мере Лебега и предложение о парадоксе Банаха-Тарского. Кроме того, опять же, в этом посте НЕТ скрытого смысла или содержания.
Я немного выгорел от написания к 17:00, и к тому времени, когда я начал этот пост, мне действительно не хотелось писать. Чтобы разобраться в некоторых вещах о Банахе-Тарском, я провел несколько фактических исследований, как в Интернете, так и в моем учебнике по математике, в котором были аннотации о мере Лебега и предложение о парадоксе Банаха-Тарского. Кроме того, опять же, в этом посте НЕТ скрытого смысла или содержания.
Нравится:
Нравится Загрузка…
Связанные
Парадокс Банаха – Тарского
Парадокс Банаха – Тарского — это теорема в теоретико-множественной геометрии, которая утверждает, что твердый шар в трехмерном пространстве может быть разбит на несколько неперекрывающихся частей, которые затем могут быть собраны вместе другим способом, чтобы получить две идентичные копии. оригинального шара. Кусочки представляют собой бесконечные разбросы точек, которые требуют бесчисленного бесконечного числа произвольных вариантов для явного определения, но процесс повторной сборки включает в себя только их перемещение и вращение без изменения формы.
В статье, опубликованной в 1924 году, Стефан Банах и Альфред Тарский дали конструкцию такого «парадоксального разложения», основанную на более ранних парадоксальных разложениях единичного интервала и сферы, выполненных Джузеппе Витали и Феликсом Хаусдорфом, и обсудили ряд вопросов. связанные вопросы, касающиеся разложения подмножеств евклидовых пространств в различных измерениях. Они доказали следующее более общее утверждение, сильную форму парадокса Банаха – Тарского:
Для любых двух ограниченных подмножеств A и B евклидова пространства по крайней мере в трех измерениях, оба из которых имеют непустую внутренность, есть разбиения A и B на конечное число непересекающихся подмножеств, A = A 1 ∪… ∪ A k , B = B 1 ∪ … ∪ B k , так что для каждого i от 1 до k наборы A i и B i совпадают.
Это неверно в измерениях один и два, но Банах и Тарский показали, что аналогичное утверждение остается верным, если разрешено счетное количество подмножеств. Разница между размерностями 1 и 2, с одной стороны, и размерностями 3 и выше, с другой стороны, обусловлена более богатой структурой группы Gn евклидовых движений в высших измерениях, которая разрешима при n = 1, 2 и содержит свободную группу с двумя образующими при n ≥ 3.Джон фон Нейман изучил свойства группы эквивалентностей, которые делают возможным парадоксальное разложение, выявив класс аменабельных групп, для которых не существует парадоксальных разложений. Он также нашел форму парадокса на плоскости, в которой вместо обычных конгруэнций используются аффинные преобразования, сохраняющие площадь.
Разница между размерностями 1 и 2, с одной стороны, и размерностями 3 и выше, с другой стороны, обусловлена более богатой структурой группы Gn евклидовых движений в высших измерениях, которая разрешима при n = 1, 2 и содержит свободную группу с двумя образующими при n ≥ 3.Джон фон Нейман изучил свойства группы эквивалентностей, которые делают возможным парадоксальное разложение, выявив класс аменабельных групп, для которых не существует парадоксальных разложений. Он также нашел форму парадокса на плоскости, в которой вместо обычных конгруэнций используются аффинные преобразования, сохраняющие площадь.
Теорема Банаха – Тарского названа парадоксальной потому, что она противоречит основной геометрической интуиции. «Удвоение шара» путем разделения его на части и перемещения их вращениями и перемещениями без растяжения, изгиба или добавления новых точек кажется невозможным, поскольку все эти операции сохраняют объем, но объем удваивается в конец.Согласно сильной версии теоремы, точки внутри горошины можно отсортировать на части, части можно вращать и собирать заново, чтобы покрыть все точки на Солнце.
Парадокс возможен в теории множеств благодаря аксиоме выбора, которая позволяет конструировать неизмеримые множества, наборы точек, не имеющих объема в обычном смысле. Роберт Соловей показал, что аксиома выбора или ее более слабый вариант необходима для построения неизмеримых множеств, построив модель теории множеств ZF (без выбора), в которой каждое геометрическое подмножество имеет четко определенную меру Лебега.
Существование неизмеримых множеств, таких как парадокс Банаха – Тарского, использовалось в качестве аргумента против аксиомы выбора, хотя большинство математиков признают существование неизмеримых множеств.
Недавно было показано, что части в разложении можно выбирать таким образом, чтобы их можно было непрерывно перемещать на место, не сталкиваясь друг с другом. [1]
Формальное лечение
Парадокс Банаха – Тарского утверждает, что шар в обычном евклидовом пространстве можно удвоить, используя только операции разбиения на подмножества, замены набора конгруэнтным набором и повторной сборки. Его математическая структура значительно проясняется за счет подчеркивания роли, которую играет группа евклидовых движений, и введения понятий равноразложимых множеств и парадоксальных множеств. Предположим, что G — группа, действующая на множестве X. В наиболее важном частном случае X — n-мерное евклидово пространство, а G состоит из всех изометрий X, то есть преобразований X в себя, которые сохраняют расстояния. Две геометрические фигуры, которые можно преобразовывать друг в друга, называются конгруэнтными, и эта терминология будет распространена на общее G-действие.Два подмножества A и B в X называются G-равноразложимыми или равноразложимыми относительно G, если A и B можно разбить на одно и то же конечное число соответственно G-конгруэнтных частей. Легко видеть, что это определяет отношение эквивалентности между всеми подмножествами X. Формально, если
Его математическая структура значительно проясняется за счет подчеркивания роли, которую играет группа евклидовых движений, и введения понятий равноразложимых множеств и парадоксальных множеств. Предположим, что G — группа, действующая на множестве X. В наиболее важном частном случае X — n-мерное евклидово пространство, а G состоит из всех изометрий X, то есть преобразований X в себя, которые сохраняют расстояния. Две геометрические фигуры, которые можно преобразовывать друг в друга, называются конгруэнтными, и эта терминология будет распространена на общее G-действие.Два подмножества A и B в X называются G-равноразложимыми или равноразложимыми относительно G, если A и B можно разбить на одно и то же конечное число соответственно G-конгруэнтных частей. Легко видеть, что это определяет отношение эквивалентности между всеми подмножествами X. Формально, если
и есть элементы g 1 , …, g k группы G такие, что для каждого i от 1 до k, g i (A i ) = Bi, тогда мы будем говорить, что A и B являются G-равносоставными из k частей. Если множество E имеет два непересекающихся подмножества A и B таких, что A и E, а также B и E являются G-равноразложимыми, то E называется парадоксальным.
Если множество E имеет два непересекающихся подмножества A и B таких, что A и E, а также B и E являются G-равноразложимыми, то E называется парадоксальным.
Используя эту терминологию, парадокс Банаха – Тарского можно переформулировать следующим образом:
Трехмерный евклидов шар равносоставлен с двумя копиями самого себя.
Фактически, в этом случае известен резкий результат (благодаря Рафаэлю М. Робинсону): удвоение мяча может быть достигнуто с помощью пяти фигур; и меньше пяти штук не хватит.
Сильная версия парадокса утверждает:
Любые два ограниченных подмножества 3-мерного евклидова пространства с непустыми внутренностями равноразложимы.
Хотя это, по-видимому, более общее, это утверждение выводится простым способом из удвоения шара с использованием обобщения теоремы Бернштейна – Шредера, принадлежащего Банаху, из которого следует, что если A равноразложимо с подмножеством B, а B равноразложимо с подмножество A, то A и B равноразложимы.
Парадокс Банаха-Тарского стал несколько менее причудливым, указав, что для двух множеств в сильной форме парадокса всегда существует биективная функция, которая может отображать точки одной формы в другую во взаимно однозначном соотношении. мода. На языке теории множеств Георга Кантора эти два множества имеют равную мощность. Таким образом, если увеличить группу, чтобы допустить произвольные биекции X, тогда все множества с непустой внутренней частью станут конгруэнтными. Точно так же мы можем превратить один шар в больший или меньший шар, растягивая, другими словами, применяя преобразования подобия.Следовательно, если группа G достаточно велика, мы можем найти G-равноразложимые множества, «размер» которых меняется. Более того, поскольку счетное множество может быть разделено на две копии самого себя, можно было ожидать, что каким-то образом использование счетного множества частей может помочь. С другой стороны, в парадоксе Банаха – Тарского количество частей конечно, а допустимые эквивалентности — евклидовы сравнения, сохраняющие объемы. Тем не менее, каким-то образом они удваивают объем мяча! Хотя это, конечно, удивительно, но некоторые из частей, используемых в парадоксальном разложении, являются неизмеримыми множествами, поэтому понятие объема (точнее, меры Лебега) для них не определено, и разбиение не может быть выполнено на практике.Фактически, парадокс Банаха – Тарского демонстрирует, что невозможно найти конечно-аддитивную меру (или меру Банаха), определенную на всех подмножествах евклидова пространства трех (и более) измерений, которая инвариантна относительно евклидовых движений и принимает значение один на единичном кубе. В своей более поздней работе Тарский показал, что, наоборот, отсутствие парадоксальных разложений этого типа влечет существование конечно-аддитивной инвариантной меры.
Тем не менее, каким-то образом они удваивают объем мяча! Хотя это, конечно, удивительно, но некоторые из частей, используемых в парадоксальном разложении, являются неизмеримыми множествами, поэтому понятие объема (точнее, меры Лебега) для них не определено, и разбиение не может быть выполнено на практике.Фактически, парадокс Банаха – Тарского демонстрирует, что невозможно найти конечно-аддитивную меру (или меру Банаха), определенную на всех подмножествах евклидова пространства трех (и более) измерений, которая инвариантна относительно евклидовых движений и принимает значение один на единичном кубе. В своей более поздней работе Тарский показал, что, наоборот, отсутствие парадоксальных разложений этого типа влечет существование конечно-аддитивной инвариантной меры.
Суть доказательства парадокса в форме «удвоения шара», представленного ниже, заключается в том замечательном факте, что с помощью евклидовой изометрии (и переименования элементов) можно преобразовать одну четверть некоторого множества (по сути, поверхность единичная сфера) на три четверти этого множества плюс одно очко.Это довольно легко следует из парадоксального разложения F 2 F 2 , свободной группы с двумя образующими. Доказательство Банаха и Тарского опиралось на аналогичный факт, открытый Хаусдорфом несколькими годами ранее: поверхность единичной сферы в пространстве представляет собой несвязное объединение трех множеств B, C, D и счетного множества E таких, что, с одной стороны, B , C, D попарно конгруэнтны, и, с другой стороны, B конгруэнтна объединению C и D. Это часто называют парадоксом Хаусдорфа.Тщательно проанализировав структуру этого аргумента, Рафаэль М. Робинсон в 1947 году доказал, что минимальное количество фигур в парадоксальном разложении шара равно пяти, полностью отвечая на вопрос, поставленный фон Нейманом в 1929 году.
Связь с более ранними работами и роль аксиомы выбора
Банах и Тарский прямо признают построение Джузеппе Витали в 1905 году множества, носящего его имя, парадокс Хаусдорфа (1914) и более раннюю (1923) статью Банаха как предшественники своей работы.Конструкции Виталия и Хаусдорфа зависят от выбранной аксиомы Цермело, которая также имеет решающее значение для статьи Банаха – Тарского как для доказательства их парадокса, так и для доказательства другого результата:
Два евклидовых многоугольника, один из которых строго содержит другой, не равносоставимы.
Они замечают:
Le rôle que joue cet axiome dans nos raisonnements nous semble mériter l’attention
(Роль, которую эта аксиома играет в наших рассуждениях, нам кажется заслуживающей внимания)
и отметим, что хотя второй результат полностью согласуется с нашей геометрической интуицией, его доказательство использует AC даже более существенно, чем доказательство парадокса.Таким образом, Банах и Тарский подразумевают, что AC не следует отвергать просто потому, что он производит парадоксальное разложение. Действительно, такой аргумент также отверг бы некоторые геометрически интуитивные утверждения!
По иронии судьбы, в 1949 году А.П. Морс показал, что утверждение о евклидовых многоугольниках может быть доказано в ZF и, следовательно, не требует аксиомы выбора. В 1964 году Пол Коэн доказал равносогласованность выбранной аксиомы с остальной частью теории множеств, из которой следует, что ZFC (теория множеств ZF с аксиомой выбора) непротиворечива тогда и только тогда, когда теория множеств ZF без выбора непротиворечива.Позже Роберт М. Соловей, используя технику принуждения Коэна, установил, что при отсутствии выбора согласованно назначать меру Лебега любому подмножеству в Rn, что противоречит BT. Результаты Соловея распространяются на ZF, дополненную слабой формой AC, называемой аксиомой зависимого выбора, DC. Отсюда следует, что
Парадокс Банаха – Тарского не является теоремой ZF или ZF + DC (Wagon, следствие 13.3).
Большинство математиков в настоящее время принимают AC из прагматических соображений.Как указывает Стэн Вагон в конце своей монографии, парадокс Банаха – Тарского более важен для своей роли в чистой математике, чем для фундаментальных вопросов. Что касается аксиомы выбора, BT играет ту же роль, что и существование неизмеримых множеств. Но парадокс Банаха – Тарского более значим для остальной математики, потому что он мотивировал новое плодотворное направление исследований — совместимость групп, которая не имеет ничего общего с фундаментальными вопросами.
В 1991 году, используя недавние результаты Мэтью Формана и Фридриха Верунга, [2] Януш Павликовский доказал, что парадокс Банаха-Тарского следует из ZF и теоремы Хана-Банаха.[3] Теорема Хана-Банаха не опирается на полную аксиому выбора, но может быть доказана с помощью более слабой версии AC, называемой леммой об ультрафильтрации. Итак, Павликовский доказал, что теория множеств, необходимая для доказательства парадокса Банаха-Тарского, хоть и сильнее, чем ZF, но слабее, чем полная ZFC.
Эскиз доказательства
По сути, парадоксальное разложение шара достигается за четыре шага:
1. Найдите парадоксальное разложение свободной группы на два образующих.
2. Найдите группу вращений в трехмерном пространстве, изоморфную свободной группе с двумя образующими.
3. Используйте парадоксальное разложение этой группы и выбранную аксиому, чтобы получить парадоксальное разложение полой единичной сферы.
4. Расширьте это разбиение сферы до разбиения единичного твердого шара.
Теперь мы обсудим каждый из этих шагов более подробно.
Шаг 1. Свободная группа с двумя образующими a и b состоит из всех конечных строк, которые могут быть образованы из четырех символов a, a -1 , b и b -1 , так что a не появляется непосредственно рядом с символом a-1 и отсутствие b появляется непосредственно рядом с ab -1 . Две такие строки можно объединить и преобразовать в строку этого типа, многократно заменяя «запрещенные» подстроки пустой строкой. Например: abab -1 a -1 , объединенный с abab -1 a, дает abab -1 a -1 abab -1 a, который сокращается до abaab -1 a.Можно проверить, что набор этих строк с помощью этой операции образует группу с нейтральным элементом — пустой строкой e. Назовем эту группу F2.
Группа F 2 может быть «парадоксально разложена» следующим образом: пусть S (a) будет набором всех строк, которые начинаются с a и определяют S (a -1 ), S (b) и S (b -1 ) аналогично. Ясно, что
, но также
и
.
Обозначение aS ( -1 ) означает взять все строки в S ( -1 ) и объединить их слева с помощью.
Убедитесь, что вы поняли эту последнюю строчку, потому что она лежит в основе доказательства. Теперь посмотрим на это: мы разрезаем нашу группу F2 на четыре части (забудьте о е, это не представляет проблемы), затем «сдвинем» некоторые из них, умножив на a или b, затем «повторно соберем» две из них. чтобы сделать F 2 и собрать два других, чтобы сделать еще одну копию F 2 .Это именно то, что мы хотим сделать с мячом.
Шаг 2. Чтобы найти группу вращений трехмерного пространства, которая ведет себя так же (или «изоморфна») группе F 2 , мы берем две ортогональные оси, например оси x и z, и пусть A будет вращением некоторого иррационального числа, кратного π, возьмем arccos (1/3) вокруг первой оси x, а B будет вращением некоторого иррационального числа, кратного π, возьмем arccos (1 / 3), около второй оси z. (Этот шаг нельзя выполнить в двух измерениях, так как он включает в себя вращение в трех измерениях.Если мы сделаем два поворота вокруг одной оси, результирующая группа будет коммутативной и не будет иметь свойства, требуемого на шаге 1.) Это несколько беспорядочно, но не слишком сложно показать, что эти два поворота ведут себя так же, как элементы a и b в наша группа F 2 . Мы его пропустим, оставив упражнение читателю. Новая группа вращений, порожденная A и B, будет называться H. Конечно, теперь у нас также есть парадоксальное разложение H.
Шаг 3. Единичная сфера S 2 разбивается на орбиты под действием нашей группы H: две точки принадлежат одной и той же орбите тогда и только тогда, когда есть вращение в H, которое перемещает первую точку во вторую.Мы можем использовать аксиому выбора, чтобы выбрать ровно одну точку с каждой орбиты; собрать эти точки в множество M. Теперь (почти) каждая точка в S 2 может быть достигнута ровно одним способом, применяя собственное вращение из H к соответствующему элементу из M, и из-за этого парадоксальное разложение H тогда получается парадоксальное разложение S 2 .
Шаг 4. Наконец, соедините каждую точку на S 2 лучом с началом координат; парадоксальное разложение S 2 2 затем дает парадоксальное разложение твердого единичного шара за вычетом центра.(Центр шара требует немного большего ухода, но мы опускаем эту часть на эскизе.)
NB. В этом наброске некоторые детали замалчиваются. Следует быть осторожным с набором точек на сфере, которые оказываются на оси некоторого вращения в H. Однако таких точек только счетное количество, и их можно заделать (см. Ниже). То же самое и с центром мяча.
Некоторые детали уточнены. На шаге 3 мы разделили сферу на орбиты нашей группы H.Чтобы упростить доказательство, мы опустили обсуждение точек, которые фиксируются некоторым поворотом; поскольку парадоксальная декомпозиция F 2 основана на смещении определенных подмножеств, то факт, что некоторые точки зафиксированы, может вызвать некоторые проблемы. Поскольку любое вращение, за исключением тождества S 2 , имеет две фиксированные точки, и поскольку H, изоморфный F 2 , является счетным, существует счетное количество точек S 2 , которые фиксируются некоторым поворотом в H. , обозначим это множество неподвижных точек D.Шаг 3 доказывает, что S 2 -D допускает парадоксальное разложение. Остается показать модель
. Иск. S 2 -D равноразборный с S 2 . Доказательство. Пусть λ — некоторая прямая, проходящая через начало координат, не пересекающая ни одну точку в D — это возможно, поскольку D счетно. Пусть J — набор углов α, таких что для некоторого натурального числа n и некоторого P в D, r (α) P также находится в D, где r — поворот вокруг λ элемента nα. Тогда J счетно, поэтому существует угол θ не в J.Пусть ρ — поворот вокруг λ на θ, тогда ρ действует на S 2 без неподвижных точек в D, т. Е. Ρn (D) не пересекается с D, а при натуральном m
Для шага 4 уже было показано, что шар без точки допускает парадоксальное разложение; Остается показать, что мяч без точки равноразложен с мячом.Рассмотрим сферу внутри шара радиуса r = половина радиуса шара, чей центр находится в r от центра шара, обозначим эту сферу S17. Тогда S17 минус точка равноразложима с S17 по утверждению, так как набор из одной точки счетно. Обратите внимание, что это включает вращение вокруг точки, отличной от начала координат, поэтому парадокс Банаха-Тарского включает изометрии евклидова 3-пространства, а не просто SO (3).
Приведенное выше доказательство требует 2 * 4 * 2 + 8 = 24 части, 2 для удаления фиксированных точек, 4 из шага 1, 2 для воссоздания фиксированных точек и 8 для центральной точки второго шара.На шаге 1 переместите {e} и все строки символа a только в S (a-1), сделайте это для всех орбит, кроме одной. Переместите {e} последней орбиты в центр второго шара. Это дает 16 + 1 штуку. Имея больше алгебры, можно также разложить фиксированные орбиты на 4 набора, как на шаге 1. Это дает 5 частей и является наилучшим возможным вариантом.
Получение бесконечного количества шаров из одного
Используя парадокс Банаха – Тарского, можно получить k копий шара в евклидовом n-пространстве из одного, для любых целых чисел и, i.е. шар можно разрезать на k частей, чтобы каждый из них можно было составить равным образом в шар того же размера, что и исходный. Используя тот факт, что свободная группа F 2 ранга 2 допускает свободную подгруппу счетно бесконечного ранга, аналогичное доказательство дает, что единичная сфера S n — 1 1 может быть разбита на счетное бесконечное число частей, каждая из которых является равноразборным (из двух частей) с S n — 1 1 с помощью вращения. Используя аналитические свойства группы вращений SO (n), которая является связной аналитической группой Ли, можно дополнительно доказать, что сфера S n — 1 может быть разбита на столько частей, сколько существует действительных чисел (т. Е. штук), так что каждая деталь может быть равносоставлена с двумя деталями согласно S n — 1 с помощью вращения.Эти результаты затем распространяются на единичный шар, лишенный начала координат.
Парадокс фон Неймана в евклидовой плоскости
В евклидовой плоскости две равносоставимые по отношению к группе евклидовых движений фигуры обязательно имеют одну и ту же площадь, поэтому парадоксальное разложение квадрата или диска типа Банаха – Тарского, использующее только евклидовы сравнения, невозможно. Концептуальное объяснение различия между плоскими и многомерными случаями было дано Джоном фон Нейманом: в отличие от группы SO (3) вращений в трех измерениях, группа G 2 евклидовых движений плоскости является разрешимой, что влечет существование инвариантной конечно-аддитивной меры на G 2 и R2 и исключает парадоксальные разложения неотъемлемых множеств.Затем фон Нейман задал следующий вопрос: можно ли построить такое парадоксальное разложение, если допустить большую группу эквивалентностей?
Ясно, что если допустить сходство, любые два квадрата на плоскости станут эквивалентными даже без дальнейшего деления. Это побуждает ограничить внимание группой SA 2 аффинных преобразований, сохраняющих площадь. Поскольку площадь сохраняется, любое парадоксальное разложение квадрата относительно этой группы было бы нелогичным по тем же причинам, что и разложение Банаха – Тарского шара.Фактически, группа SA 2 содержит в качестве подгруппы особую линейную группу SL (2, R), которая, в свою очередь, содержит свободную группу F 2 с двумя образующими в качестве подгруппы. Это делает правдоподобным, что доказательство парадокса Банаха – Тарского можно имитировать на плоскости. Основная трудность здесь заключается в том, что единичный квадрат не инвариантен относительно действия линейной группы SL (2, R), следовательно, нельзя просто перенести парадоксальное разложение с группы на квадрат, как на третьем шаге приведенное выше доказательство парадокса Банаха – Тарского.Кроме того, неподвижные точки группы представляют много трудностей (например, начало координат фиксируется при всех линейных преобразованиях). Решение фон Неймана состояло в том, чтобы расширить группу до SA 2 , включив переводы, и он построил парадоксальное разложение единичного квадрата относительно увеличенной группы. Применяя метод Банаха – Тарского, парадокс для квадрата можно усилить следующим образом:
Любые два ограниченных подмножества евклидовой плоскости с непустыми внутренностями равноразложимы относительно сохраняющих площадь аффинных отображений.
Класс групп, выделенных фон Нейманом в ходе изучения феномена Банаха – Тарского, оказался очень важным для многих областей математики: это аменабельные группы или группы с инвариантным средним, включающие все конечные и все разрешимые группы. Вообще говоря, парадоксальные разложения возникают, когда группа, используемая для эквивалентностей в определении равноразложимости, не поддается.
Последние достижения
* Статья фон Неймана оставила открытой возможность парадоксального разложения внутренней части единичного квадрата относительно линейной группы SL (2, R) (Вагон, вопрос 7.4). В 2000 году Миклош Лацкович доказал, что такое разложение существует. [4] Точнее, пусть A — семейство всех ограниченных подмножеств плоскости с непустой внутренней частью и на положительном расстоянии от начала координат, а B — семейство всех плоских множеств, обладающих тем свойством, что объединение конечного числа переносится под некоторые элементы SL (2, R) содержит проколотую окрестность начала координат. Тогда все множества в семействе A SL (2, R) -эквивалентно разложимы, как и множества в B. Отсюда следует, что оба семейства состоят из парадоксальных множеств.
* В течение долгого времени было известно, что полная плоскость парадоксальна по отношению к SA2, и что минимальное количество частей будет равно четырем при условии, что существует локально коммутативная свободная подгруппа SA2. В 2003 году Кензи Сато создал такую подгруппу, подтвердив, что четырех пьес достаточно. [5]
См. Также
* Задача Тарского о квадрате окружности
Банкноты
1.Локально коммутативная свободная группа, действующая на плоскости, Fundamenta Mathematica, 180 (2003), no. 1, 25–34.
Ссылки
* Стефан Банах и Альфред Тарски, Sur la décomposition des ensembles de points en membersment congruentes, Fundamenta Mathematicae, 6, (1924), 244–277. Обзор на JFM
* Справочник непрофессионала по парадоксу Банаха – Тарского (от Kuro5hin)
* Карл Стромберг, Парадокс Банаха-Тарского, Amer.Математика. Месяц 86 (1979), нет. 3, 151–161.
* Фрэнсис Э. Су, «Парадокс Банаха – Тарского»
* Джон фон Нейман, Zur allgemeinen Theorie des Masses, Fundamenta Mathematicae, 13 (1929), 73–116.
* С. Вагон, Парадокс Банаха-Тарского, Cambridge University Press, 1986.
* Л. Вапнер, Горох и Солнце: математический парадокс, A.K. Петерс, 2005
Парадокс Банаха-Тарского | Великая стратегия: вид из Орегона
Пятница
G Несмотря на поразительные, но все же очевидные последствия парадокса Банаха-Тарского, это тот вид вещей, к которому ум регулярно возвращается, чтобы насладиться этим интеллектуальным удовлетворением.Неназванный автор книги «Справочник непрофессионала по парадоксу Банаха-Тарского » объясняет парадокс следующим образом:
Парадокс гласит, что можно взять твердую сферу («шар»), разрезать ее на конечное количество частей, переставить их, используя только вращения и перемещения, и собрать их в две идентичные копии оригинала. сфера. Другими словами, вы удвоили объем исходной сферы.
T Вся запись на Wolfram Mathworld выглядит следующим образом:
Впервые сформулированный в 1924 году парадокс Банаха-Тарского гласит, что можно разделить шар на шесть частей, которые можно собрать жесткими движениями, чтобы сформировать два шара того же размера, что и оригинал.Впоследствии Робинсон (1947) сократил количество пьес до пяти, хотя пьесы чрезвычайно сложны. (Пять частей минимальны, хотя четырех частей достаточно, если пренебречь единственной точкой в центре.) Обобщение этой теоремы состоит в том, что любые два тела в R 3 , которые не простираются до бесконечности и каждое содержит шар произвольного размера можно разрезать друг на друга (т.е. они равносоставимы).
T Вышеупомянутый Справочник непрофессионала по парадоксу Банаха-Тарского пытается дать интуитивный толчок к этому удивительному результату теории множеств (используя аксиому выбора или какое-либо эквивалентное предположение) и заключает это показательный комментарий:
На самом деле, если задуматься, это не более странно, чем то, как нам удалось продублировать набор всех целых чисел, разделив его на две половины и переименовав элементы в каждой половине, чтобы каждый из них стал идентичным оригиналу. установить снова.Вполне логично, что мы можем постоянно извлекать все больше объема из бесконечно плотной математической сферы S.
B До того, как я прочитал это сегодня, я никогда не встречал такого ясного и лаконичного изложения парадокса Банаха-Тарского, которое дает пищу для размышлений. Можем ли мы продолжить это извлечение объема с помощью чего-то вроде процесса трансфинитной рекурсии, придя к некоему геометрическому эквиваленту ε 0 ? Это интересный вопрос, но я начал не думать о нем как о подходящем для философски настроенного математика.
W Когда я сегодня думал о парадоксе Банаха-Тарского, я начал задаваться вопросом, можно ли применить достаточно обобщенную формулировку парадокса к онтологии в целом, чтобы мы могли продемонстрировать (возможно, не с математической строгостью, но лучше всего, что можно продемонстрировать в онтологии), что весь мир можно разложить на конечное число частей, а затем снова собрать на два или более идентичных мира.
W Используя процитированный выше интуитивный глянец, мы можем сказать, что это возможно, поскольку мир онтологически бесконечно плотен.Что это могло значить? Что было бы для мира быть онтологически плотным, как бесконечные множества бесконечно плотными? Что ж, такого рода вопросы выходят далеко за пределы интуиции и, следовательно, приводят нас к открытой структуре языка, которая может адаптироваться к новым вариантам использования, но не имеет «естественного» значения тем или иным образом. Открытая текстура даже наших формальных языков делает его похожим на зыбучие пески: если у вас нет прочной связи с твердой землей, вы, скорее всего, упадете прочь, пока не уйдете под воду.Именно по этой причине Кант искал критического анализа разума, чтобы разум не выходил за свои собственные границы, которые (как выразился Стросон) являются пределами смысла.
B Как бы осторожно мы ни относились к беспрецедентным обычаям, мы также должны приветствовать их как возможность превзойти интуицию, в конечном счете укоренившуюся в самой почве, из которой мы возникли. Я много раз на этом форуме утверждал, что наши идеи в конечном итоге происходят из ландшафта, в котором мы живем, посредством образа жизни, навязанного нам этим ландшафтом.Но мы не ограничиваемся тем, что нам завещало наше происхождение. У нас есть сила превзойти наши земные корни, и если это происходит за счет случайной путаницы и дезориентации, пусть будет так.
S o Я предполагаю, что, хотя не существует «правильного» ответа на вопрос, можно ли считать мир онтологически бесконечно плотным, мы можем дать ответ на этот вопрос, и мы действительно можем привести рациональные и последовательные аргументы в пользу нашего ответа. если только мы заставим себя прилагать усилия для размышления о незнакомых мыслях — всегда полезное интеллектуальное упражнение.
I Итак, мир онтологически бесконечно плотен? Является ли мир повсюду непрерывным, чтобы его действительно можно было описать с помощью классической теории, такой как общая теория относительности? Или мир в конечном итоге является зернистым, так что его следует описывать неклассической теорией, такой как квантовая механика? На еще более абстрактном уровне можно ли сказать, что существа мира имеют какую-либо плотность, если мы не ограничиваем существ пространственно-временными существами, так что наша онтология является достаточно общей, чтобы охватить как пространственно-временные, так и непространственные -временной? Это опять же, как обсуждалось выше, вопрос создания рационально защищаемой конвенции.
У меня в настоящее время нет ответа на этот вопрос. Не следует ожидать, что онтологические загадки откроются для нескольких минут случайного размышления. Я вернусь к этому и снова подумаю. Когда-нибудь — вряд ли когда-нибудь в ближайшее время, но когда-нибудь, тем не менее, — я могу найти способ размышления о проблеме, который отдает должное вопросу о бесконечной плотности существ в мире.
Мне не кажется, что это настолько диковинно, как кажется.Две из наиболее распространенных идиом, которые можно найти в современной аналитической философии, когда такие философы предпочитают не говорить на технических идиомах, — это «мебель вселенной» и «резание природы на стыках». Оба эти выражения удивительно выразительны, и, более того, они, кажется, указывают на концепцию мира как существенно дискретного. Другими словами, они предполагают абсолютную онтологическую прерывность. Если бы за этим можно было внимательно следить, мы могли бы ответить на поставленный выше вопрос отрицательно, но сам факт того, что мы могли бы ответить на вопрос отрицательно, говорит о двух важных вещах:
1 ), что вопрос может, по крайней мере в некотором смысле, быть значимым и, следовательно, как философски значимый и заслуживающий нашего внимания, и…
2 ), если на вопрос можно ответить отрицательно, вполне вероятно, что для утвердительного ответа на вопрос можно было бы найти достаточно логичные аргументы.
T Парадокс Банаха-Тарского парадоксален, по крайней мере отчасти, потому что , а не , кажется, «вырезает природу на стыках». Это нарушение нашей геометрической интуиции происходит в результате развития других интуиций, и в конечном итоге парадоксальным является столкновение интуиций. Кант утверждал, что между моральными обязанностями не может быть конфликта; параллельно с этим можно было бы принять постулат естественного разума о том, что не может быть конфликта между интеллектуальными интуициями.Хотя, насколько мне известно, этот принцип не был явно сформулирован, это предположение, повсеместно присутствующее в наших рассуждениях (то есть, это интуиция по поводу наших предположений). Такие убедительные парадоксы, как парадокс Банаха-Тарского (или, если на то пошло, большинство результатов теории множеств), напоминают нам об ограничениях нашей интуиции в дополнение к напоминанию об ограниченности нашей геометрической интуиции.
. . . . .
Фракталы и геометрическая интуиция
1.Бенуа Мандельброт, R.I.P.
2. Вопрос для математиков, склонных к философии
3. Фракталы и парадокс Банаха-Тарского
4. Внутреннее ощущение эпсилон нуля
5. Приключения геометрической интуиции
6. Заметка о фракталах и экстракции Банаха-Тарского
7. Геометрическая интуиция и эпистемическое пространство
.. . . .
. . . . .
. . . . .
Нравится:
Нравится Загрузка …
Парадокс Банаха-Тарского — Скачать PDF бесплатно
1 Университет Осло, проект MAT2 Парадокс Банаха-Тарского Автор: Фредрик Мейер Руководитель: Надя С.Ларсен Аннотация В своей слабой форме парадокс Банаха-Тарского утверждает, что для любого шара в R можно разделить его на конечное число частей, собрать их, используя только вращения, и получить два новых шара того же размера, что и исходный шар. . В своей сильной форме парадокс утверждает, что для любых двух ограниченных множеств A, BR с непустой внутренней частью можно разбить A, переместить части и получить B. Для парадоксального разбиения сферы это можно показать, что 4 штуки на самом деле достаточно.Эта короткая статья направлена на доказательство парадокса Банаха-Тарского в его слабой и сильной формах вместе с только что упомянутой нижней оценкой числа частей в разложении. 2 мая
2 Введение Понятие бесконечности всегда было хорошо известно как средство создания, казалось бы, парадоксальных ситуаций. Одним из известных примеров является то, что мощность Z равна мощности 2Z, даже если одно является правильным подмножеством другого.Пример, более похожий на досуг, следующий: Лемма. (Отель Парадокс). Предположим, у вас есть отель с бесконечным количеством номеров. Предположим далее, что все комнаты заняты. Тогда, если приедет новый гость, для него еще найдется место. Доказательство. Пусть гость из комнаты номер n будет переведен в комнату номер n +. Это смещение в бесконечность оставляет номер комнаты свободным. Сформулируем основную цель статьи: Теорема 2 (сильный парадокс Банаха-Тарского). Для любых двух ограниченных множеств A, B с непустой внутренней частью можно разделить A на конечное число частей, переместить части и получить B.Несмотря на то, что парадокс Банаха-Тарского может показаться невероятным, это вряд ли. Идеи, использованные в доказательствах, ведущих к этой теореме, в основном основаны на той же идее, что и в доказательстве Hotel Paradox. Это более простое доказательство показывает основную идею нескольких доказательств, ведущих к парадоксу: Теорема .. Единичная окружность с удаленной точкой S \ {pt} может быть разделена на две части A, B, так что после поворота B к B имеем AB = S. Доказательство. Отождествим единичный круг с {z C z =}.Без ограничения общности можно предположить, что удаленная точка есть. Наша цель — создать некий бесконечный набор, который, как в Hotel Paradox, позволяет нам двигаться в сторону бесконечности. Итак, пусть B = {e in n N}. Поскольку 2π иррационально, это множество бесконечно (и, в частности, все члены множества различны). Пусть A = (S \ {pt}) \ b. Ясно, что S \ {} = A B. Теперь повернем B, используя изометрию ρ (z) = e iz. Это порождает набор B = {e in n N {}}. Таким образом, S = A B. Обратите внимание на смещение техники к бесконечности.Читателю стоит развлечься, ища, где используется та же идея. При этом парадокс Банаха-Тарского небезынтересен — отнюдь не так. Процитирую Вагона []: Идеи, вытекающие из парадокса Банаха-Тарского, стали основой теории конечно-аддитивных мер
3 теория, которая включает тесное взаимодействие между анализом (теория меры и линейные функционалы), алгеброй (комбинаторная теория групп), геометрией (группы изометрий) и топологией (локально компактные топологические группы).Наконец, нужно помнить, что, хотя R очень похож на пространство, в котором мы живем и дышим, они принципиально отличаются: R имеет бесчисленное количество элементов, но наше пространство, скорее всего, имеет конечное количество элементов (таким образом, такие чудеса, как кормление четырех тысяч человек, маловероятны ). Предполагается, что читатель знаком с некоторой линейной алгеброй и некоторыми основами теории групп. Также будут использоваться определения счетности и несчетности. 2 Парадокс Банаха-Тарского Напомним, что группа G действует на множестве X, если существует биекция GXX такая, что gg 2 x = g (g 2 x) и x = x для g, g 2 G где обозначает личность Г.Чтобы добавить некоторой субстанции к слову парадоксальный, мы сформулируем его определение: Определение 2 .. Пусть G — группа, действующая на непустом множестве X. Предположим, что существует множество EX такое, что существуют попарно непересекающиеся подмножества A, …, A n, B …, B m из E и g, …, gn, h, …, hm G такие, что E = ngj A j = j = Мы говорим, что E G-парадокс. m h j B j. Заметим, что если H — подгруппа группы G, а множество X H-парадоксально, то X автоматически G-парадоксально. Каждая группа естественным образом действует на себя посредством левого перевода. Мы будем говорить, что группа G парадоксальна, если она G-парадоксальна, когда действие остается переводом.Нам будет важен наш первый пример парадоксального множества: j = Лемма 2.2. Свободная группа F 2 второго порядка парадоксальна. Доказательство. Пусть a, b — образующие F 2. Пусть W (ρ) — множество всех слов в F 2, начинающихся с ρ слева. Тогда W (a) W (a) W (b) W (b) {e} = F 2 и эти множества попарно не пересекаются. Тогда F 2 = W (a) aw (a). Ведь если w / W (a), то a w W (a), поэтому w = a (a w) aw (a). Аналогично F 2 = W (b) bw (b). Если парадоксальная группа G действует на множестве X особенно хорошо, можно снять парадокс с группы на множество: 2
4 Лемма 2.. Если G парадоксален и действует на X без нетривиальных неподвижных точек, то X G-парадоксален. Доказательство. Пусть A i, B i, g i, h i такие же, как в определении 2. Используя аксиому выбора, выберем такое множество M, что M содержит ровно один элемент из каждой G-орбиты в X; тогда {g M: g G} является дизъюнктным разбиением X: Конечно, g G g M = X, так как M содержит по одному элементу из каждой G-орбиты. Чтобы доказать дизъюнктность, предположим, что существуют такие g, h G, что g M h M. Тогда существуют x, y M такие, что g x = h y. Тогда h g x = y, поэтому x и y находятся на одной G-орбите, но по нашему выбору M это означает, что x = y.Итак, мы имеем h g x = x. Поскольку G действует на X без нетривиальных неподвижных точек, это означает, что h g =, а значит, должно быть равно. Пусть теперь A j = g A j {g M} (j =, …, n) и B j = g B j {g M} (j =, …, m). Очевидно, A, .. ., A n, B, …, B m — непересекающиеся подмножества X (поскольку A i и B j не пересекаются). Мы утверждаем, что X = n j = g j A j = m j = h j B j, доказывая, что X является G-парадоксальным. Например, предположим, что x X. Поскольку M содержит по одному элементу из каждой G-орбиты, существует g G такой, что x g M. Поскольку G парадоксальна, мы знаем, что g = g j a j для некоторого a j A j.Таким образом, x g j (a j M), и поскольку a j M A j, мы видим, что x n j = g j A j. Случай для B j s, конечно же, идентичен. Непосредственным следствием предыдущей леммы является следующее Следствие 2.4. Если F 2 действует на X без нетривиальных неподвижных точек, то X является F 2 -парадоксальным. Напомним, что SO () — группа вращений сферы или, что то же самое, группа -матриц A таких, что det A =. Наш следующий результат окажется рецептом любого парадоксального разложения. Лемма 2.5. Есть вращения A и B вокруг прямых, проходящих через начало координат в R, порождающие подгруппу SO (), изоморфную F 2, свободной группе двух образующих.
5 Доказательство. Пусть A ± = и B ± = ± ± — наши два вращения. Теперь пусть w — сокращенное слово в A ±, B ±, которое не является пустым словом I. Мы утверждаем, что w не может действовать как тождество на R, тем самым доказывая, что A, BF 2, где A, B — подгруппа в SO (), порожденная A, B. Сначала отметим, что без ограничения общности мы можем считать, что w оканчивается на A ± (так как если бы w было пустым словом, то сопряжение с помощью A ± не изменит этого).Мы утверждаем, что w = k a b 2 c, где a, b, c Z и b и k — длина слова w, и в этом случае w не может действовать как тождество на R. Мы докажем это индукцией по k. Базовый случай k = прост. Тогда по предположению w = A ±: w = = 2 2 ± 2 2 ± 2 2 = ± 2 2 Конечно, k = в порядке. Теперь пусть w = A ± w или w = B ± w, где w = a k b 2, c a, b, c Z и b не делится на. Несложный расчет показывает, что w = k A ± {}} {2 2 ± 2 2 ab 2 c = k = a 4b 2 (bk ± 2a) = ackb 2. c 4 ± a 2 2. a 4b + b 2 c
6 Аналогично для w = B ± w.Имеем: {a = a 4b, b = b ± 2a, c = c, если w = A ± wa = a, b = b 2c, c = c ± 4b, если w = B ± w () Очевидно, a, b , c Z. Мы должны показать, что b, и все будет готово: случай w = A ± B ± v (где, возможно, v = I). Тогда w = A ± B ± v, так что согласно () имеем b = b ± 2a = b ± 6a. Поскольку по предположению b, следует, что b. Случай 2 w = B ± A ± v. Доказано как случай. Случай w = A ± A ± v. По предположению v = k 2 a b 2 c, где a, b, c Z и b. Из () следует, что b = b ± 2a = b ± 2 (a 4b) = b + b ± 2a 9b = 2b 9b, поэтому b.Случай 4 w = B ± B ± v. Этот случай рассматривается как выше. Наша слабая цель — показать, что S 2 SO () — парадоксален. То есть вы можете разделить сферу так, чтобы вращение частей производило две новые копии S 2. Следующий результат показывает, что это почти возможно. Лемма 2.6 (парадокс Хаусдорфа). Существует счетное подмножество D в S2 такое, что S 2 \ D является SO () — парадоксальным. Доказательство. Пусть A и B такие, как в предыдущем доказательстве. Пусть G = A, B F 2, поэтому G парадоксален. Поскольку A и B вращаются вокруг начала координат, каждое w G \ {I} имеет ровно две неподвижные точки.Пусть D будет совокупностью всех 5
7 точек в S2, которые фиксируются некоторым w G \ {I}. Поскольку G счетно, то же самое и D. Ясно, что G действует на S 2 \ D без нетривиальных неподвижных точек: ведь если p S 2 \ D и g G и g p = p, то мы имели бы p D, что невозможно. По лемме 2 следует, что S 2 \ D G-парадоксально. Поскольку G SO (), заключаем, что S 2 \ D является SO () — парадоксальным. Любой прямоугольник можно разрезать пополам и переместить, чтобы получился равнобедренный треугольник.Мы говорим, что прямоугольник и равнобедренный треугольник равносоставимы. Это понятие можно обобщить на множества, над которыми действуют группы. Определение 2.7. Предположим, что G — группа, действующая на множестве X, и что A, B X. Тогда A и B называются G-равноразложимыми (мы пишем AGB), если существуют подмножества A i множества A и B i множества B такие, что nn A = A i = A, B = B i, (2) i = и A i A j = = B i B j для ij, и gi G такие, что gi A i = B i для каждого i {, 2, … , n}. Когда из контекста станет ясно, о какой группе идет речь, мы напишем A B вместо A G B.Позже мы будем использовать обозначение A n B, когда A и B равноразложимы с использованием n частей. Для нас будет важно убедиться, что G действительно является отношением эквивалентности и, таким образом, разбивает P (X), множество степеней X. Лемма 2.8. G — отношение эквивалентности на подмножествах P (X). Доказательство. Очевидно, A G A. Пусть тождество G действует на самом A. Итак, G рефлексивен. Теперь предположим, что A G B. Мы должны показать, что также B G A. Поскольку A G B, существует такое разбиение A и B, что g i A i = B i для каждой ячейки в разделе.Но тогда мы имеем, что A i = gi (g i A i) = gi B i для каждой ячейки в разделе. Таким образом, B G A. Значит, G симметрична. Чтобы показать транзитивность, предположим, что A G B и B G C. Сначала заметим, что если A B =, то ga gb =. В противном случае существовали бы a A и b B такие, что ga = gb, но это означает, что a = b, что невозможно (поскольку A B =). Теперь, поскольку AGB, существует разбиение A = ni = A i и B = ni = B i такое, что gi A i = B i для in и gi G. И поскольку BGC существует разбиение B = mj = Bj и C = mj = C j такие, что hj B j = C j для jm и hi G.Теперь заметим, что, поскольку m B i = (B j) m B i = (B i B j), j = 6 j = i =
8 имеем gi A i = mj = (bi B j), откуда, по нашему наблюдению, следует, что {gi (B i B j) in, jm} является непересекающимся разбиением A. Таким образом, поскольку B j = ni = (B i B j), то hjgi (gini = (B i B j)) = C j. Мы заключаем, что A G C. Обратите внимание, что в приведенном выше доказательстве мы использовали не более nm частей.Простое, но, тем не менее, очень важное наблюдение по поводу этой связи: Лемма 2.9. Если A A 2 = = B B 2 с A B и A 2 B 2, то A A 2 B B 2. Доказательство. AB означает, что B = gi A i для некоторого разбиения A и gi G, и аналогично B 2 = gj A j 2. Тогда, поскольку AA 2 =, мы можем использовать то же разбиение AA 2, что и в A, A 2. Результат следует. Равноразложимость упрощает определение парадоксальности множества: Лемма 2 .. Предположим, что G — группа, действующая на множестве X, а E и E — G-равноразложимые подмножества X.Если E G-парадоксально, то E. Доказательство. Предположим, что E G-парадоксален. Тогда существуют A i, B i E и gi, hi, как в определении 2. где A = n A j и B = j = где nj = gi A i = E и mj = hj B j = E. Тогда AGE и BG E. Поскольку G является отношением эквивалентности, оно транзитивно, поэтому, поскольку EGE, у нас есть AGE и BG E. Но из определения равносоставимости это означает, что существуют такое разбиение A j множества A и элементы группы ki, что E = jk JA j, а также разбиение B j множества B и элементы группы kj такие, что E = jk JB j.Но это означает, что E парадоксален. Следующий результат показывает, что если вы удалите любой счетный набор точек из сферы, вы всегда можете восстановить его с помощью вращения. m j = B j 7
9 Лемма 2 .. Если D — счетное подмножество S 2, то S 2 SO () S 2 \ D. Доказательство. Пусть L — прямая, проходящая через начало координат, такая что L D =. Теперь определим следующим образом: ρ — это поворот на L на угол nθ W = θ [, 2π) для некоторого целого числа n такого, что если x D ρ x D Поскольку D счетно, то и W.Следовательно, существует элемент α [, 2π) \ W. Пусть ρ — поворот вокруг L на угол α. Из определения W следует, что ρ n D D = для всех целых n N. Отсюда следует, что ρ n D ρ m D = (n, m N, n m). () Пусть теперь D = n = ρn D. Заметим, что в силу () ρ D \ D = D. Тогда S 2 = D (S 2 \ D) ρ D (S 2 \ D) = S 2 \ D , по желанию. Обратите внимание на использование леммы 2.9. Следствие 2.2. S 2 — это SO () — парадоксально. Доказательство. Объединение лемм 2.6, 2. и 2. немедленно дает нам результат: лемма 2.6 говорит нам, что существует счетное подмножество D S 2 такое, что S 2 \ D является SO () — парадоксальным.Лемма 2. сообщает нам, что S 2 \ D SO () S 2, и в сочетании с леммой 2 получаем, что S 2 является SO () — парадоксальным. Обозначим через O множество всех евклидовых изометрий, сохраняющих хиральность, то есть множество всех перемещений и поворотов. Слабый парадокс Банаха-Тарского — более сильное утверждение, чем следствие 2.2. Лемма 2. (Слабый парадокс Банаха-Тарского). Каждый замкнутый шар в R O -парадоксален. Доказательство. Без ограничения общности мы докажем только, что замкнутый единичный шар B [, R] парадоксален. Доказательство для любого другого шара идентично, но более беспорядочно.Сначала покажем, что B [, R] \ {} парадоксален. Поскольку S 2 SO () — парадоксально, существуют A, …, A n, B, …, B m S 2 R и g, …, gn, h, …, hm SO ( ) как в определении 2. Пусть A j = {tx t (,], x A j} (j =, …, n) 8
10 и B j = {tx t (,], x B j} (j =, …, m). Отметим, что A i A j = при ij и что B [, R] \ {} = ngj A j = j = mhj Bj Из определения парадоксальности следует, что B [, R] \ {} действительно парадоксален.Пусть теперь x = (,, 2) B [, R] \ {}. Пусть ρ — вращение бесконечного порядка вокруг прямой, проходящей через x, а не через начало координат. Пусть D = {ρ n n N}. Очевидно, что ρ D = D \ {}. Тогда по более ранним результатам: B [, R] = D (B [, R] \ D) ρ D (B [, R] \ D) = B [, R] \ {}. По лемме 2 следует, что B [, R] SO () — парадоксально, а SO () является подгруппой в O. j = Практически идентичное доказательство дает нам следующее: Следствие 2.4. R парадоксален. Однако нам нужна более удивительная математика. На нашем пути к сильной форме парадокса нам понадобится следующее очень важное наблюдение: Лемма 2.5. Если A G B, то существует биекция f: A B такая, что C f (c) всякий раз, когда C A. Доказательство. Поскольку AB, существует такое разбиение A = ni = A i и B = ni = B i, что gi A i = B i для gi G. Теперь определим f: AB следующим образом: f (x) = gix if x A i Поскольку AB, эта функция включена, и это очевидно, поскольку она определяется групповыми действиями. Таким образом, f — биекция. Чтобы доказать последнюю часть утверждения, предположим, что C A. Тогда A i C дает нам разбиение C. Поскольку f (c) = ni = gi (A i C), из определения равносложности следует, что C f ( в).Определим отношение следующим образом: 9
11 Определение 2.6. Пусть G — группа, действующая на множестве X, и пусть A, B X. Если A G B, где B B, мы пишем A G B. Как и в случае с G, мы будем писать A B вместо A G B, если это упрощение не вызывает путаницы. Очевидно, G рефлексивна. Чтобы доказать транзитивность, предположим, что A B и B C. Тогда A B для некоторого B B. По лемме 2.5 B f (b) C, поэтому A B f (b) C.Таким образом, A C. На самом деле мы имеем, что если A B и B A, то A B. Другими словами, это антисимметричное бинарное отношение. Таким образом определяется частичный порядок на -классах P (X). Теорема 2.7 (теорема Банаха-Шредера-Бернштейна). Предположим, G — группа, действующая на множестве X. Если A, B X, A G B, B G A, то A G B. Доказательство. Пусть f: A B (B) и g: B A (A) — биекции, что гарантируется леммой 2.5. Пусть C = A \ A и индуктивно определим C n + = gf (c n), где g f: A A, и пусть C = n = C n. Мы утверждаем, что A \ C = g (b \ f (c)). Итак, предположим, что x B \ f (C).Тогда мы не можем иметь g (x) C n для любого n>, поскольку это означало бы, что x f (c n). Таким образом, g (b \ f (c)) A \ C. Теперь заметим, что A \ C = A \ C. Итак, предположим, что x A \ C. Тогда существует y B такое, что g (y) = x. Если бы y f (c), мы имели бы g (y) = x C, что невозможно, поэтому y B \ f (C). Таким образом, A \ C g (b \ f (c)). Итак, A \ C = g (b \ f (c)). По нашему определению g это означает, что A \ C B \ f (C). Таким же образом C f (c). Итак, A = (A \ C) C (B \ f (C)) f (c) = B по лемме 2.9. Теорема Банаха-Шредера-Берштейна дает нам характеристику парадоксальных множеств в терминах равноразложимости: Лемма 2.8. Пусть G — группа, действующая на множестве X, и пусть E X. Тогда E G-парадоксально тогда и только тогда, когда существуют непересекающиеся A, B такие, что A B = E и A E B. Доказательство. Мы уже знаем, что если E G-парадоксален, то мы можем найти непересекающиеся A, B такие, что AE B. Осталось показать, что мы можем найти такие A, B, что AB = E и такие, что свойства A, B все еще держит. Пусть f: E A — биекция, как гарантируется леммой 2.5. Тогда, поскольку f (e \ b) A и f (e \ b) E \ B, мы видим, что E \ B A, поэтому E \ B E. И поскольку E A E \ B, имеем E E \ B.Таким образом, по теореме Банаха-Шредера-Бернштейна E E \ B. Итак, выберите A = E \ B и B = B.
12 Обратное утверждение верно по определению парадоксальности. Наконец-то мы разработали достаточно механизмов, чтобы представить сильную форму парадокса: Теорема 2.9. Если A и B — ограниченные подмножества R, каждое из которых имеет непустую внутренность, то A B. Доказательство. По теореме Банаха-Шредера-Бернштейна достаточно показать, что AB, поскольку симметричный аргумент дает противоположное соотношение.Поскольку A ограничен, мы можем выбрать шар K так, чтобы A K. Поскольку B имеет непустую внутренность, мы можем выбрать шар L такой, что L B. Для некоторого достаточно большого n, K может быть покрыт n перекрывающимися копиями L. То есть выберите переводы ti такие, что K ni = ti L. Теперь выберите переводы ti такие, что ti L tj L = для ij, и пусть S = ni = ti L. Затем, используя слабый парадокс Банаха-Тарского, скопируйте L n раз получим LS, и в частности S L. Тогда AK ni = ti LSLB, что вместе с леммой 2.5 доказывает утверждение.На этом наша работа над существованием парадоксальных разложений завершена. Минимизация количества частей Остальная часть этой статьи будет сосредоточена на минимизации количества частей, необходимых для парадоксального разложения сферы. Хотя сам парадокс может быть достаточно интересным, знание того, сколько штук достаточно, интересно из-за интуитивно удивительной низкой границы этого числа. Фактически, количество частей, необходимых для парадоксального разложения сферы, равно 4. Во-первых, давайте формально определим число r, которое мы хотим минимизировать: Определение.. Предположим, что G действует на X и E, A, B X. Тогда E G-парадоксально с использованием r частей, если A B = с A B = E таким, что где m + n = r. A m E n B Из леммы 2.2 мы помним, что F 2 парадоксален, но в нашем доказательстве мы не использовали все F 2 для демонстрации парадоксальности. Однако это возможно, как утверждает следующая лемма:
13 Лемма 2. Пусть F 2 — свободная группа, порожденная элементами a, b.Тогда мы можем найти такое разбиение A, …, A 4 F 2, что A b A 2 = F 2 и A a A 4 = F 2, что означает, что F 2 парадоксален при использовании этого разбиения. Более того, для любого w F 2 разбиение может быть выбрано таким, чтобы w находилось в той же ячейке, что и единица F 2. Это простое доказательство, найденное в []. Доказательство. Предположим, что w — слово, начинающееся, скажем, с ρ = a. Доказательство для любого другого ρ идентично (замените a где бы то ни было на ρ). Определим A i следующим образом: (где W (ρ) обозначает множество всех слов, начинающихся с ρ) A = W (b) A 2 = W (b) A = W (a) \ {ann N} A 4 = W (a) {ann N} {} Теперь аналогично доказательству леммы 2.2, мы имеем F 2 = A b A 2. Показать, что F 2 = A a A 4, лишь немного сложнее. Ясно, что все степени a включены в A 4. Итак, предположим, что w не является степенью a. Тогда если w / W (a), a w W (a). Отсюда следует, что w = a (a w) a W (a). Таким образом, F 2 парадоксально состоит из четырех частей. Ясно также, что, w A 4. Имеется четырехкомпонентный аналог леммы 2: лемма .. Пусть F 2 действует на X без нетривиальных неподвижных точек. Тогда X является F 2 -парадоксальным с использованием четырех кругов. Доказательство. Доказательство идентично доказательству леммы 2.(обратите внимание, что при поднятии парадокса на набор сохраняется количество частей). Просто используйте разбиение F 2, данное в лемме 2. Если G действует на X и x X, пусть Stab (x) = {σ G σ x = x}. Концепция доказательства основного результата этого раздела заключается в следующем: Ключевое Определение 4. Действие группы G на множестве X называется локально коммутативным, если Stab (x) коммутативна для любого x X. Эквивалентно, если два элемента G имеют общую неподвижную точку, то они коммутируют. Мы уже встречались с локально коммутативными действиями. Возьмем группу вращений сферы S 2; если два поворота имеют общую фиксированную точку, они должны иметь общую ось и, таким образом, коммутировать.2
14 Лемма 5. Пусть F 2 действует на X так, что действие локально коммутативно. Тогда X является F 2 -парадоксальным с использованием четырех частей. Доказательство. Это долгое и трудное доказательство, но мы скоро получим свою награду. Мы будем использовать лемму 2, чтобы разделить X на A, A 2, A, A 4, такие, что b A 2 = A 2 A A 4 и a A 4 = A A 2 A 4, что достаточно для доказательства теоремы. Мы разместим каждый элемент X на орбите A i по орбите (возможно, используя разные разбиения F 2 для разных орбит).Заметим, что все F 2 -орбиты в X либо состоят только из неподвижных точек, либо из нетривиальных неподвижных точек: предположим, что gx = x для x X и g F 2. Если y F 2 x, то y = hx для некоторого h F 2. Тогда hgh y = hgh (hx) = hg x = hx = y, поэтому y — неподвижная точка. Для точек на орбитах, не состоящих из неподвижных точек, такое же назначение точек выполняется просто. Для каждой орбиты зафиксируйте любой представитель x. Тогда каждый элемент y в орбите может быть однозначно записан как y = v x с v F 2. Теперь применим лемму 2 к разбиению F 2, обладающему дополнительным свойством, что и w лежат в одной и той же ячейке разбиения.Поместите y в A i, если v A i F 2. Для орбит, полностью состоящих из неподвижных точек, нам нужно работать больше. Зафиксируем орбиту O. Пусть w — слово минимальной длины, фиксирующее точку x в O. Пусть ρ — самая левая буква в w. Мы видим, что w не может заканчиваться на ρ, поскольку в противном случае ρ wρ зафиксировало бы ρ x и было бы короче w. Мы утверждаем, что любую точку y O можно записать однозначно как v x, где v не заканчивается на w или ρ. Зачем? Пусть v — минимальное слово такое, что y = v x. Мы видим, что v не может заканчиваться на w или w, потому что это противоречит тому, что v является словом минимальной длины (и w, и w фиксируют x).Если, однако, v заканчивается на ρ, мы выбираем vw, не заканчивающуюся на w или ρ (потому что ρ — первая буква в w). Мы покажем, что единственными элементами, фиксирующими x, являются степени w. Здесь и появляется локальная коммутативность. Предположим, что u фиксирует x (в дополнение к w). Тогда по локальной коммутативности wu = uw. Но поскольку F 2 свободен, это означает, что w = t k и u = t l для некоторых целых чисел k, l и t F 2 (иначе у нас было бы нетривиальное соотношение для букв F 2). Из минимальности w следует, что k 15 Уникальность представления y = v x вытекает легко: предположим, что y = v x = u x — оба представления желаемой формы (v не должно заканчиваться на w, ρ). Тогда u v x = x, поэтому одно из u v или v u является положительной степенью w.Предположим, без ограничения общности, что это u v; тогда u v = w n для некоторого целого n. Поскольку w начинается с ρ, u должно начинаться с ρ (что противоречит нашему предположению, что u не заканчивалось на ρ), или u сокращается против v, что означает, что v заканчивается на w (что противоречит нашему предположению, что v не заканчивалось на ρ), и мы заключаем, что u = v. Установив, что каждое y O может быть однозначно записано как y = vx, мы помещаем y в A i, если v A i F 2. Чтобы показать, что это сопоставление работает, сначала рассмотрим отношение b A 2 A 2 AA 4. Предположим, y A 2. Тогда y имеет представление y = vx для x на орбите с v A 2.Теперь рассмотрим b y. Если bv y — правильное представление b y, то, поскольку v A 2 влечет bv A 2 A A 4, b y должным образом помещается в A 2 A A 4. Но bv может оканчиваться на w или ρ. Итак, предположим, что bv оканчивается на w. Поскольку v не заканчивается на w, bv должно быть равным w, поэтому b y = w x = x. Поскольку bv A 2 A A 4, то и w, и по нашему выбору разбиения F 2, так и есть. Поскольку x — единственное представление x, отсюда следует, что x и, следовательно, b y = bv x = w x = x лежит в A 2 A A 4. Предположим теперь, что bv оканчивается на ρ. Поскольку v нет, v должно быть равно.Тогда y = x, bv = b и, значит, ρ = b, и, исходя из нашего выбора ρ, w начинается с b. Поскольку = v A 2, по нашему выбору разбиения F 2, w A 2 также, следовательно, bw A 2 AA 4. Поскольку bw x является единственным представлением bx (обратите внимание, что w начинается с b), мы имеем by = bx A 2 AA 4. Аналогичная обработка работает для других контейнеров b (A 2 AA 4) A 2, a A 4 AA 2 A 4 и a (AA 2 A 4) A, завершая доказательство. Изучив себя предыдущим доказательством, мы можем с гордостью представить основной результат этого раздела.Парадоксально, что сфера S 2 состоит только из 4 частей, и если вы когда-нибудь попытаетесь улучшить это число, у вас ничего не получится. Теорема 6. S 2 — это SO () — парадоксальное использование четырех частей, и четыре не могут быть улучшены. Доказательство. Поскольку действие вращений на сфере локально коммутативно (по рассуждению в предыдущем абзаце), а SO () имеет подгруппу, изоморфную F 2, первая часть утверждения следует из леммы 5. Чтобы продемонстрировать, что композицию из четырех частей нельзя улучшить, предположим противное: что S 2 содержит два непересекающихся подмножества A, B таких, что A m X n B, где m + n <4.По крайней мере, одно из m или n должно быть равно. Если 4 16 m =, то S 2 = g (a) для некоторого g SO (), откуда A = g (S 2) = S2 и B =; противоречие. И мы останавливаемся здесь. Ссылки [] Стэн Вагон, Парадокс Банаха-Тарского, Cambridge University Press, 985. [2] Фолькер Рунде, Лекции о приемлемости, Лекции по математике, 774, Springer Verlag, 22. [] Фрэнсис Эдвард Су, Парадокс Банаха-Тарского , Малая диссертация, часть PhD, Гарвардский университет, 99.[4] Роберт М. Френч. Теорема 2 Банаха-Тарского, The Mathematical Intelligencer, вып. 4, Springer-Verlag New York, 988. Стандартный текст по теме. Он содержит (почти) все, что вы когда-либо захотите узнать о парадоксе. Он также содержит множество открытых проблем, связанных с парадоксом. 2 Популярное введение в идеи, лежащие в основе доказательства теоремы. Именно здесь я обнаружил понятие смещения к бесконечности, как упоминалось во введении. 5 Вчера мы слушали появление Патрика Хоннера в подкасте «Моя любимая теорема».Хоннер обсуждал теорему Вариньона. Мы уже обсуждали это появление раньше, но дети еще не слушали подкаст: Делюсь с детьми выступлением Патрика Хоннера «Моя любимая теорема» Послушав подкаст, я спросил старшего сына, какая ему любимая теорема: Слушал сегодня появление @MrHonner на @myfavethm с мальчиками. Подумав, что было бы весело провести с ними завтра проект «Моя любимая теорема», я попросил их любимую теорему.Старший сын сказал: «Сфера Банаха-Тарского». Ха-ха. . . столько за идею 🙂 — Майк Лоулер (@mikeandallie) 17 марта 2018 г. Однако, отказавшись от этой идеи вначале (!), Я просмотрел страницу Википедии, посвященную парадоксу Банаха-Тарского, и нашел идею, которая, как я думал, может сработать. Вот страница: Страница Википедии о парадоксе Банаха-Тарского Идея заключалась в том, чтобы поделиться с детьми первым шагом в доказательстве — исследованием графа Кэли.Вот картинка из Википедии: Итак, вот что я сделал. Сначала я познакомил мальчиков с некоторыми основными идеями о свободной группе на двух генераторах. Я использовал кубик Рубика как для демонстрации идей, так и для демонстрации того, почему кубик Рубика не совсем подходит для идеальной демонстрации (я знаю, что эта часть видео немного затягивается, но оставайтесь с ней — есть приятный сюрприз) : Далее мы поговорили о свободной группе с двумя генераторами более подробно.Мой младший сын случайно придумал фантастический пример, который помог прояснить, как работает эта бесплатная группа. Затем возникло неожиданное заблуждение, которое я обнаружил случайно. Это привело к еще одному важному уточнению. Итак, совершенно случайно у нас состоялся отличный разговор. В последнем видео они, ребята, думали, что «буквы» можно использовать только один раз. В начале этого видео я уточнил правила. Затем мы начали говорить о представлении нашей свободной группы графом Кэли из Википедии, изображенном выше. Мне было очень интересно услышать, как мальчики описывают то, что они видели на этом графике. Наконец, мы рассмотрели два разных способа разбить граф Кэли на части. Это видео немного длинное, но в нем представлена упрощенная версия основной идеи парадокса Банаха-Тарского. Первое разложение графа Кэли на 5 частей -> элемент идентичности, слова, начинающиеся с, слова, начинающиеся с, слова, начинающиеся с, и слова, начинающиеся с.Это разложение довольно легко увидеть на картинке. Второе и очень удивительное разложение выглядит следующим образом: Комбинация (i) слов, которые начинаются с и (ii) умножение (слева) всех слов, начинающихся с, дает весь набор. То же самое верно и для комбинации (i) слов, начинающихся с и (ii) умножения (слева) всех слов, начинающихся с Хотя слова, описывающие это разложение, могут не сразу обрести смысл, вы увидите, что у мальчиков было несколько вопросов о том, что происходит, и в конце концов они смогли увидеть, как работает это второе разложение. И это второе разложение преподносит огромный сюрприз -> мы взяли 4 подмножества, объединили их попарно и создали две точные копии исходного набора. Та да 🙂 Это невероятно интересный проект, которым можно поделиться с детьми. Я очень удивлен, что любые идеи, связанные с парадоксом Банаха-Тарского, доступны детям, но простые идеи о графике Кэли действительно доступны. Используя эти идеи, вы можете показать основную идею парадокса сфер, не погружаясь полностью в группы вращения, которые, на мой взгляд, немного более абстрактны и трудны для понимания. В любом случае, это было круто! Нравится Загрузка … Упрощенная версия парадокса Банаха-Тарского для детей — Mike’s Math Page
Нравится:
Парадокс Банаха-Тарского
. Лучшие подкатегории
Лучшие подкатегории
Лучшие подкатегории
Лучшие подкатегории
Лучшие подкатегории
Лучшие подкатегории




 к. они оказываются одинаково правомерными.
к. они оказываются одинаково правомерными. Противоречие в том, что с одной стороны, это можно сделать, так как есть наименьшее число, названное в этой книге. Исходя из него, можно назвать и наименьшее неназванное. Но тут возникает проблема: континуум является несчётным, между двумя любыми числами можно вставить ещё бесконечное множество промежуточных чисел. С другой стороны, если бы мы могли назвать это число, оно автоматически бы перешло из класса неупомянутых в книге, в класс упомянутых [2].
Противоречие в том, что с одной стороны, это можно сделать, так как есть наименьшее число, названное в этой книге. Исходя из него, можно назвать и наименьшее неназванное. Но тут возникает проблема: континуум является несчётным, между двумя любыми числами можно вставить ещё бесконечное множество промежуточных чисел. С другой стороны, если бы мы могли назвать это число, оно автоматически бы перешло из класса неупомянутых в книге, в класс упомянутых [2]. В то же время
В то же время  – Пермь, 2012.
– Пермь, 2012.